Решите и объясните решение задачи:
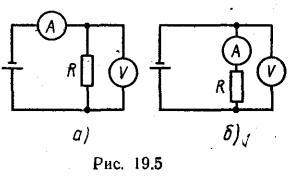
Какая из схем, изображенных на рив. 19.5, а, б, более пригодна для измерения больших сопротивлений и какая — для измерения малых сопротивлений? Вычислить погрешность, допускаемую
при измерении с помощью этих схем сопротивлений R1
= 1 кОм и R2 = 10 Ом. Принять сопротивления вольтметра Rв и амперметра
Ra соответственно равными 5 кОм и 2 Ом.
Ответ: Для схемы а) 16,7%; 0,2%. Для схемы б) 0,2%
20%
Ответы
Ответ:
Схема на рисунке а) более пригодна для измерения малых сопротивлений, так как в этом случае измеряемое сопротивление подключено параллельно вольтметру, имеющего относительно высокое внутреннее сопротивление, которое практически не повлияет на результат измерений. Схема на рисунке б), напротив, более пригодна для измерения больших сопротивлений, так измеряемое сопротивление подключено последовательно с амперметром, имеющего относительно малое внутреннее сопротивление, которое практически не повлияет на результат измерений. Дла расчета погрешности измерений для обоих схем, запишем их исходные данные.
Дано:
R1=1 кОм;
Rв=5 кОм;
R2=10 Ом;
Ra=2 Ом.
Найти g1, g2, g1', g2'.
Для схемы на рис а, относительная погрешность измерений, при измерении сопротивления R1, будет равна:
g1=(((R1*Rв/R1+Rв)-R1)/R1)*100%=((1*5/1+5)-1)/1=((5/6-1)/1)*100=16,7 %;
При измерении сопротивления R2=10 Ом, относительная погрешность измерений будет равна:
g2=(((R2*Rв/R2+Rв)-R2)/R2)*100%=((10*5*10^3/10+5*10^3)-10)/10)*100%=(9,98-10)/10)*100%=0,2%;
Для схемы на рис. б, при измерении сопротивления R1, относительная погрешность измерения, будет равна:
g1'=(((R1+Ra)-R1)/R1)*100%=(((1*10^3+2)-1*10^3)/1*10^3)*100%=(2/1*10^3)*100%=0,2%.
При измерении сопротивления R2, относительная погрешность измерений, будет равна:
g2'=(((Ra+R2)-R2)/R2)*100%=(((10+2)-10)/10)*100%=(2/10)*100%=20%.
Обжъяснение: