Предмет: Математика,
автор: lyovademyanov
задание по матанализу
Приложения:

Ответы
Автор ответа:
0
Решение.
Решаем методом подстановки .
Приложения:
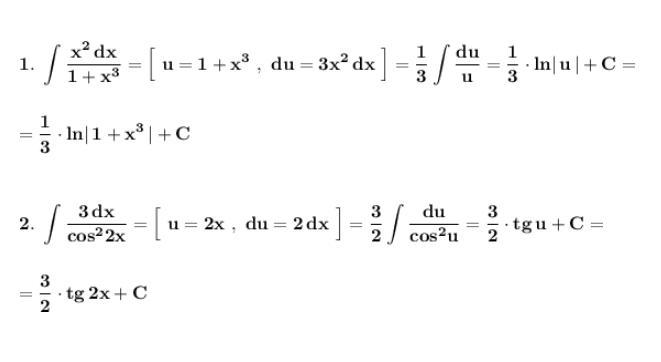
Похожие вопросы
Предмет: Биология,
автор: Ivankaiva
Предмет: Математика,
автор: lifetime2849
Предмет: Українська мова,
автор: wamycrr
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Falker2611