Question

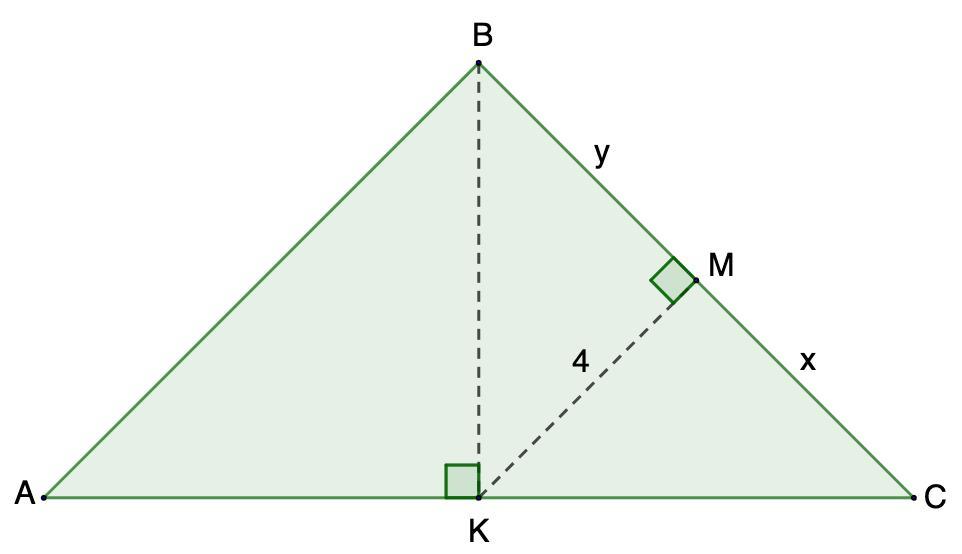
ABC равнобедренный треугольник, BK высота.Какова наименьшая площадь треугольника АВС, если длина прямой КМ от точки К до наклона ВС равна 4

Answer 1

Ответ:

Наименьшая площадь треугольника равна 32 ед.²

Пошаговое объяснение:

ABC равнобедренный треугольник, BK высота.Какова наименьшая площадь треугольника АВС, если длина прямой КМ от точки К до наклонной ВС равна 4.

Дано: ΔАВС - равнобедренный.

ВК - высота;

КМ = 4.

Найти: наименьшую площадь ΔАВС.

Решение:

Рассмотрим ΔКВС - прямоугольный.

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ КМ ⊥ ВС

Пусть СМ = х, ВМ = у

• Квадрат высоты, опущенной из вершины прямого угла на гипотенузу, равен произведению проекций катетов на гипотенузу.

⇒ КМ² = СМ · ВМ

16 = ху   ⇒  у = 16/х

• Площадь треугольника равна половине произведения стороны на высоту, которая проведена к этой стороне.

S(ΔКВС) = 1/2 · ВС · КМ = 1/2 · (х + у) · 4 = 2(х + у)

Рассмотрим ΔАВС - равнобедренный.

• Высота, проведенная из вершины к основанию, делит равнобедренный треугольник на два равных треугольника.

⇒    $\displaystyle S(ABC) = 2S(KBC) = 4(x + y) = 4\left(x + \frac{16}{x} \right)$

Получили функцию S(x).

Найдем наименьшую площадь.

Найдем производную, приравняем к нулю и найдем корни.

$\displaystyle S'(x)=4\left(1-\frac{16}{x^2} \right)=4\left(\frac{(x-4)(x+4)}{x^2} \right)\\\\x=4;\;\;\;\;\;x=-4;\;\;\;\;\;x\neq 0$

Отметим их на числовой оси и определим знаки производной на промежутках.

$+++[-4]---(0)---[4]+++$

• Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке  - минимум.

⇒ x max = -4;     x min = 4

При х = 4 функция S(x) будет иметь наименьшее значение.

Найдем наименьшую площадь ΔАВС:

$\displaystyle S(ABC)=4\left(4+\frac{16}{4}\right)=32$

Наименьшая площадь треугольника равна 32 ед.²

#SPJ1