Предмет: Геометрия,
автор: 1234567890dasha25032
Допоможіть будь ласка, даю 100 балів
Приложения:

Ответы
Автор ответа:
1
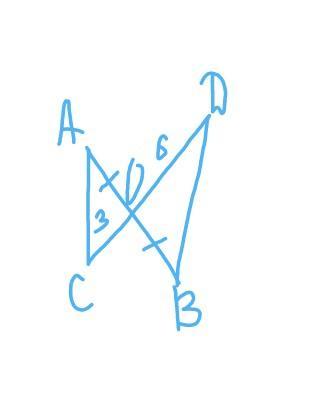
Дано, що точка О є серединою відрізка АВ. Це означає, що ОА = ОВ, і відрізок АО ділить відрізок ВО на дві рівні частини.
Ми знаємо, що СО = 3 см і DO = 6 см. Оскільки ОА = ОВ, то АО = ВО = (3 + 6)/2 = 4,5 см.
Тепер ми можемо знайти площі трикутників AOC і BOD, використовуючи формулу площі трикутника:
Площа трикутника = (Основа × Висота) / 2.
У трикутнику AOC ОА є основою, а висота є СО. Тому площа трикутника AOC дорівнює:
Площа AOC = (ОА × СО) / 2 = (4,5 см × 3 см) / 2 = 13,5 см².
Аналогічно, у трикутнику BOD ОВ є основою, а висота є DO. Тому площа трикутника BOD дорівнює:
Площа BOD = (ОВ × DO) / 2 = (4,5 см × 6 см) / 2 = 13,5 см².
Отже, площі трикутників AOC і BOD однакові і становлять 13,5 см². Відношення їх площ дорівнює 1:1
Ми знаємо, що СО = 3 см і DO = 6 см. Оскільки ОА = ОВ, то АО = ВО = (3 + 6)/2 = 4,5 см.
Тепер ми можемо знайти площі трикутників AOC і BOD, використовуючи формулу площі трикутника:
Площа трикутника = (Основа × Висота) / 2.
У трикутнику AOC ОА є основою, а висота є СО. Тому площа трикутника AOC дорівнює:
Площа AOC = (ОА × СО) / 2 = (4,5 см × 3 см) / 2 = 13,5 см².
Аналогічно, у трикутнику BOD ОВ є основою, а висота є DO. Тому площа трикутника BOD дорівнює:
Площа BOD = (ОВ × DO) / 2 = (4,5 см × 6 см) / 2 = 13,5 см².
Отже, площі трикутників AOC і BOD однакові і становлять 13,5 см². Відношення їх площ дорівнює 1:1
1234567890dasha25032:
Дякую)
Автор ответа:
2
Объяснение:
СО=3 см
DO=6 см
AO=BO=x см
∠АОС=∠ВОD=α - как вертикальные.
S(AOC)=1/2•CO•AO•sinα=1/2•3•x•sinα=
=(3x•sinα)/2
S(BOD)=1/2•DO•BO•sinα=1/2•6•x•sinα=
=3x•sinα
S(AOC)/S(BOD)=(3x•sinα)/2:(3x•sinα)=
=(3x•sinα)/2•1/(3x•sinα)=1/2
ответ: 1/2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: bekhruzzzkhasanovvv
Предмет: Алгебра,
автор: dikhtyarroman
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: lemonmur
Предмет: Химия,
автор: alexxeyshay