Question

Алгебра. Даю 10 балів.

Виконати 1 завдання.

Answer 1

Відповідь:

Пояснення:

ec663765e0d1a6b20770cc560563a489.pdf

Answer 2

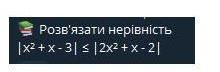
Решить неравенство

|x²+x-3| ≤ |2x²+x-2|

Объяснение:

Тк обе части положительные, то возведем обе части неравенства в квадрат

|x²+x-3|²≤ |2x²+x-2|²,

 (x²+x-3)²≤ (2x²+x-2)²,

(x²+x-3)²-(2x²+x-2)²≤ 0, по формуле разности квадратов

(х²+x-3-2x²-x+2)•(x²+x-3+2x²+x-2)≤ 0,

(-х²-1)(3х²+2х-5)≤ 0. Нулями второго

множителя являются числа -5/3 и 1.

-1(х²+1)•3•(х+5/3)(х-1)≤0 .

Метод интервалов ( учтём, что (х²+1)>0 для любого х).

Для х=10, значение левой части отрицательно, далее знаки чередуются

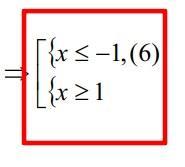
- - - [-5/3]+ + + [1]- - -

х ∈(- беск; -5/3] и [1; + беск)