Question

СРОЧНОО!! ДАЮ 50 БАЛОВ!
Площа прямокутника дорівнює 108 дм², а діагональ 15 дм. Знайдіть сторони прямокутника. СРОК СДАЧИ СЕГОДНЯ!!! ПОМОГИТЕ ПОЖАЛУЙСТА!!!

Answer 1

Ответ:

на фото

Объяснение:

Answer 2

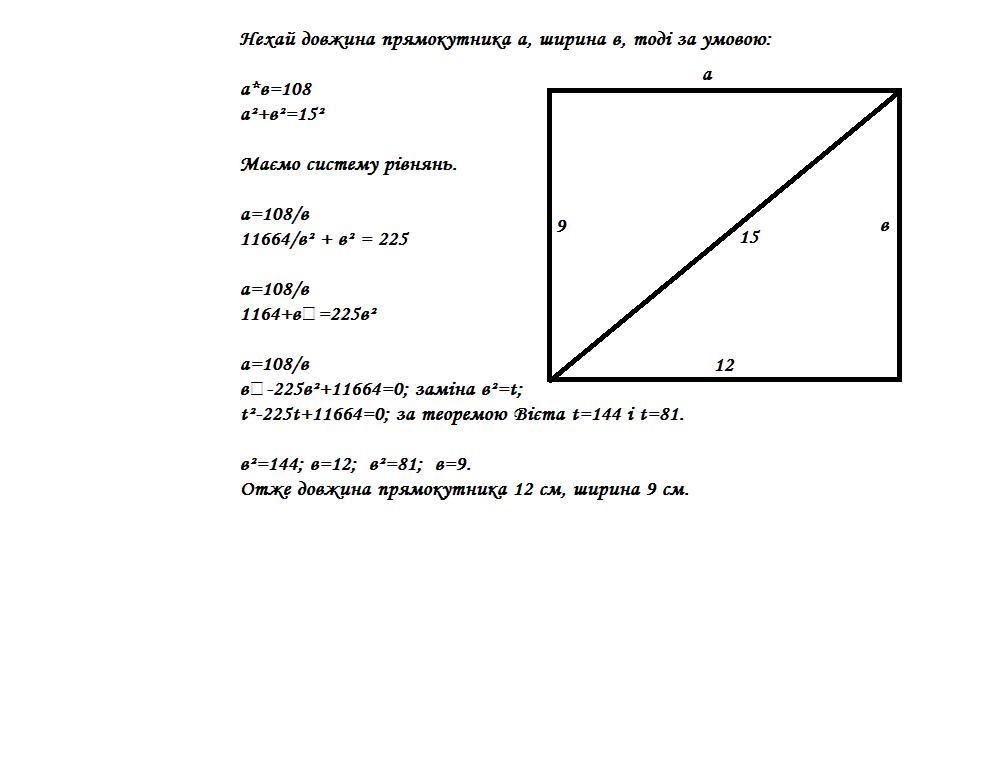
Ответ:

Объяснение:

Нехай сторони прямокутника -  х (дм)  і у(дм), діагональ ділить прямокутник навпіл і є гипотенузою трикутника . Згідно т. Піфагора (сума квадратів катетів, дорівнює квадрату гипотенузи) маємо:

х² + у² = 15²

А площа прямокутника дорівнює: S = х * у, підставимо у формулу площу і отримаємо

108 = х * у

Маємо систему рівнянь:

{х² + у² = 15²

{х * у = 108 | * 2

{x² + y² = 225

{2xy = 216

Складемо обидва рівняння:

х² + 2ху + у² = 441

(х + у) ² = 441

х + у = ±21

х + у = -21 не підходить згідно умови задачі

Тому вирішуемо наступне:

х + у = 21

х = 21 - у

Підставимо у друге рівняння:

у * (21 - у) = 108

21у - у ² = 108

у² - 21 у + 108 = 0

D = 21² - 4 * 108 = 441 - 432 = 9

√9 = 3

у₁ = (21 + 3) /2 = 12

у₂ = (21 - 3)/2 = 9

х₁ = 21 - у = 21 - 12 = 9

х₂ = 21 - у = 21 - 9 = 12

Тобто маємо прямокутник зі сторонами 12дм і 9дм

Площа дорівнює: 12 * 9 = 108 дм²