Question

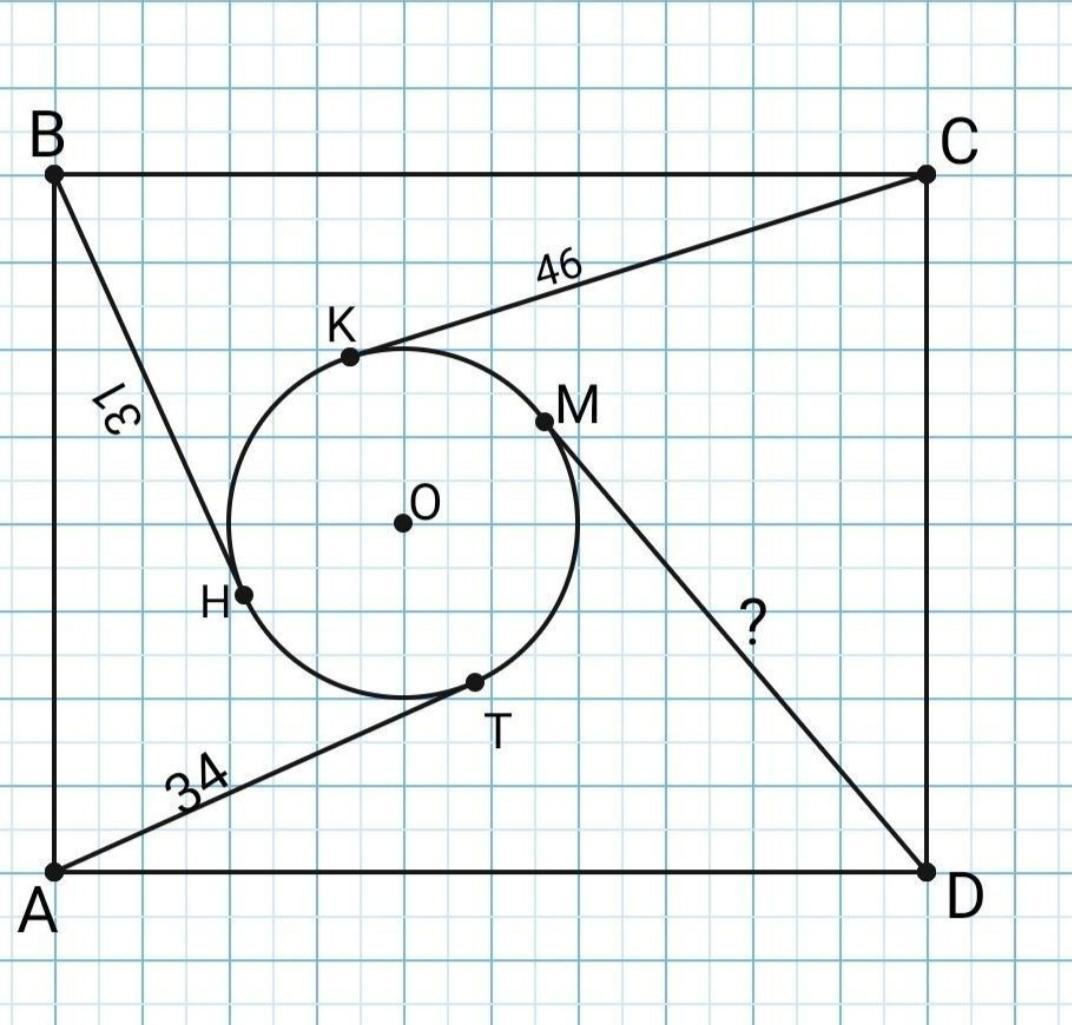
В прямоугольнике ABCD окружность с центром в точке О, к ней из вершин прямоугольника проведены касательные СК=46см; ВН=31см; АТ=34см, найдите касательную DM.

Answer 1

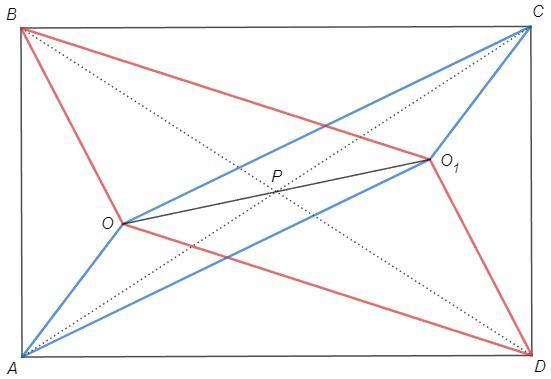
Докажем, что суммы квадратов расстояний от произвольной точки до противоположных вершин прямоугольника равны.

O - произвольная точка (не обязательно внутри прямоугольника)

Докажем: AO^2+CO^2=BO^2+DO^2

Возьмем точку O1, симметричную точке O относительно пересечения диагоналей прямоугольника P.

Видим два параллелограмма с равными диагоналями: AOCO1 и BODO1.

По тождеству параллелограмма (сумма квадратов сторон равна сумме квадратов диагоналей):

2(AO^2+OC^2) = AC^2+OO1^2 =BD^2+OO1^2 =2(BO^2+OD^2)

=> AO^2+CO^2=BO^2+DO^2

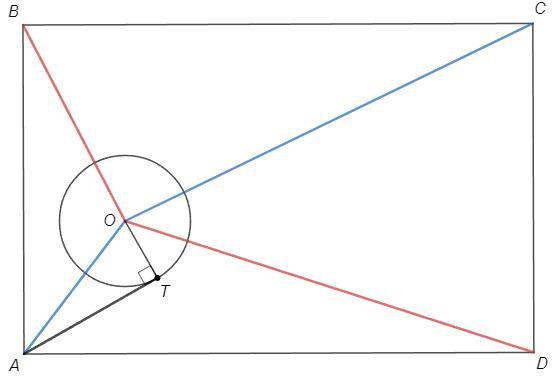
△AOT, BOH, COK, DOM, т Пифагора

AO^2 =AT^2 +r^2

BO^2 =BH^2 +r^2

CO^2 =CK^2 +r^2

DO^2 =DM^2 +r^2

AO^2+CO^2=BO^2+DO^2 => AT^2+CK^2=BH^2+DM^2

=> 34^2 +46^2 =31^2 +DM^2 => DM=√2311