Предмет: Алгебра,
автор: valihonovsaid37
Расположите числа в порядке убывания:
а=√101 + √103
b=√99 + √105
c=19.9
Ответы
Автор ответа:
1
Ответ:
Cравним числа .
Так как функция возрастающая функция , то
Cравним сначала квадраты чисел а и b . Знак - это знак сравнения , который потом превратится в знак ">" , или "<" , или "=" .
Теперь сравним числa b и с .
Окончательно получим
Приложения:
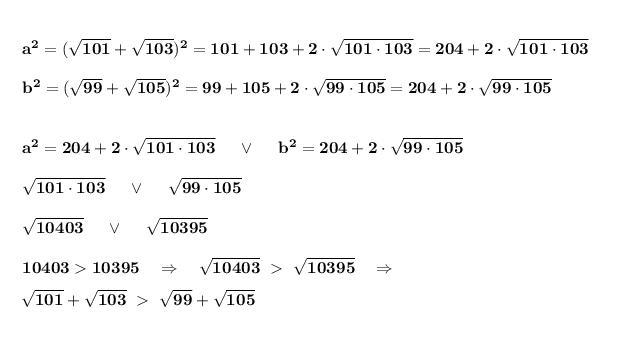

Похожие вопросы
Предмет: Математика,
автор: diianaa21
Предмет: Литература,
автор: anacerednik31
Предмет: Математика,
автор: nodirrahmatullaev3
Предмет: Геометрия,
автор: FloverCrimson
Предмет: Физика,
автор: potapov4740982