Предмет: Алгебра,
автор: xurshedxon23
найдите площадь формы графика функции у=х³-6х²+9х+1 и касательная к ней в точке х=3
Ответы
Автор ответа:
1
Ответ: 6.75 кв. ед.
Объяснение:
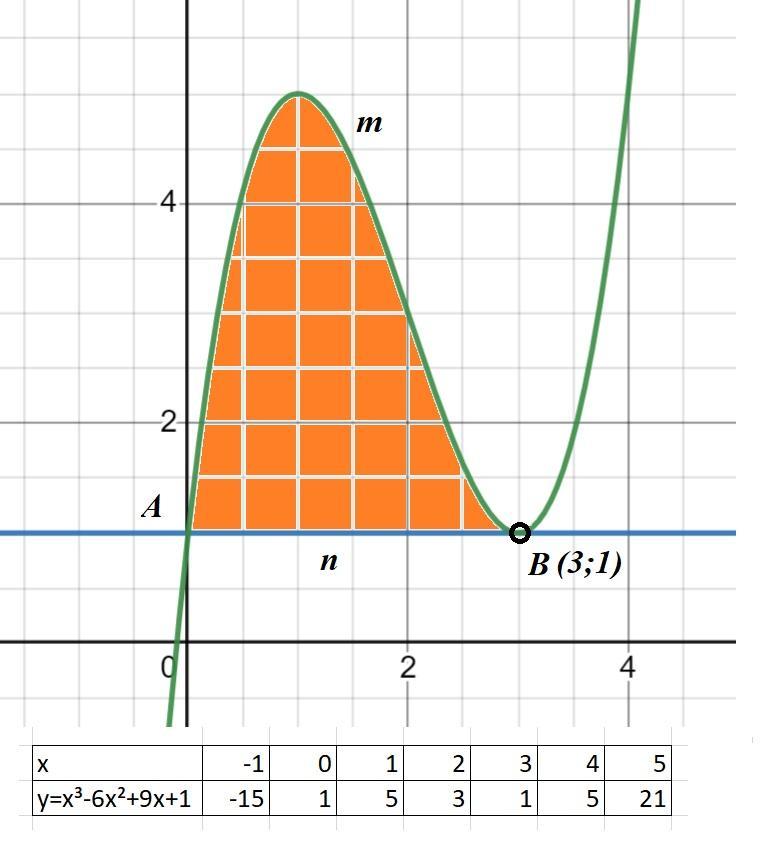
Строим график функции у=х³-6х²+9х+1.
и касательную к ней в точке х=3. (См. скриншот)
Площадь криволинейной трапеции определяем по формуле Ньютона-Лейбница
s=∫ₐᵇf(x)dx = F(x)|ₐᵇ=F(b) - F(a).
Пределы интегрирования a=0; b=3.
S=s(AmB) - s(AnB) = ∫₀³(х³-6х²+9х+1)dx - ∫₀³(1)dx = 9.75 - 3 = 6.75 кв. ед.
1) ∫₀³(х³-6х²+9х+1)dx = ∫₀³(x³)dx - 6∫₀³(x²)dx + 9∫₀³(x)dx + ∫₀³1*dx =
= 1/4(x⁴)|₀³ - 6/3(x³)|₀³+9/2(x²)|₀³+(x)|₀³ =
= 1/4(3⁴-0⁴) - 2(3³-0³) +9/2(3²-0²)+(3-0) = 81/4-2*27+81/2+3=
= 20.25 - 54 + 40.5 + 3 = 9.75 кв. ед.
2) ∫₀³(1)dx =(x)|₀³ = (3-0) = 3 кв. ед.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kovalevamargared
Предмет: Немецкий язык,
автор: katanaumenko38
Предмет: История,
автор: vladislavameln99
Предмет: Физика,
автор: frerannerpro