допоможіть будь ласка

Ответы
Решение.
ABCD - параллелограмм .
Углы параллелограмма относятся как 7 : 5 .
Значит на тупой угол приходится 7 частей , а на острый угол приходится 5 частей .
Сумма острого и тупого углов параллелограмма равна 180° , тогда
7х+5х = 180° , 12х = 180° , х = 15°
Тупой угол параллелограмма равен 7х = 7·15° = 105° ,
острый угол параллелограмма равен 5х = 5·15° = 75° .
∠A = ∠С = 75° , ∠B = ∠D = 105°
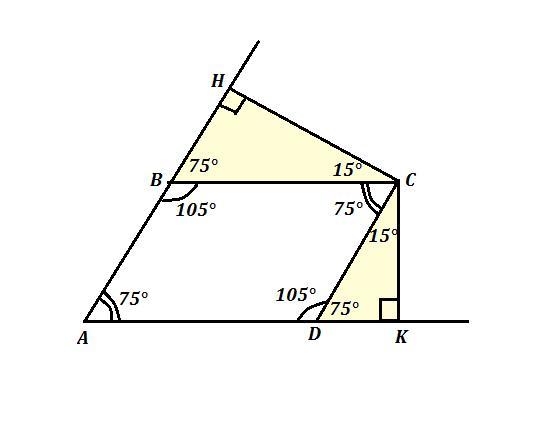
Проведём высоты из острого угла C : СН ⊥ АВ , CK ⊥ AD . Основания высот будут падать на продолжение сторон параллелограмма .
Получим прямоугольные треугольники : ΔВСН и ΔCDK .
Так как ∠СВН смежен с ∠АВС , то ∠СВН = 180°-∠АВС = 180°-105°=75°
В прямоугольном ΔСВН найдём ∠ВСН :
∠ВСН = 90°-∠СВН = 90°-75° = 15°
Аналогично, в ΔCDK угол ∠CDK = 180°-∠ADC = 180°-105°=75° ,
∠DCK = 90°-∠∠CDK = 90°-75°=15°
Найдём угол между высотами .
∠HCK = ∠ВСН + ∠ВСD + ∠DCK = 15°+75°+15° = 105°
P.S. Можно запомнить, что угол между высотами параллелограмма, проведёнными из его острого угла , равен тупому углу параллелограмма , а угол между высотами параллелограмма, проведёнными из его тупого угла , равен острому углу параллелограмма .