Question

Найдите площадь фигуры, ограниченной линиями: у = 3х^2 и у =5х + 2.

Answer 1

Ответ:

Объяснение:

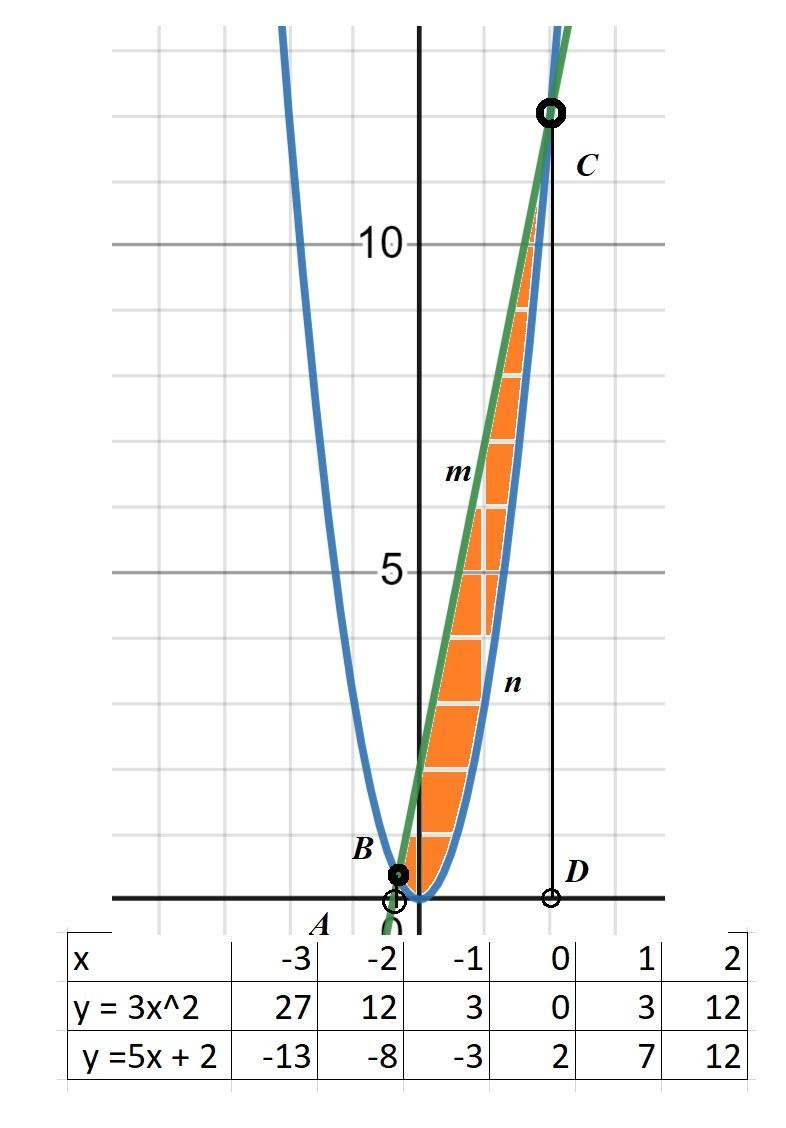
Строим графики функций

у = 3х^2;  у =5х + 2.  (См. скриншот)

S=s(ABmCD) - s(ABnCD)

s=∫ₐᵇf(x)dx.

Находим пределы интегрирования. Приравниваем правые части функций:

3х^2 =5х + 2.

3x²-5x-2 = 0;

a=3;  b=-5;  c=-2.

D=b²-4ac = (-5)²-4*3*(-2) = 25+24 = 49>0 - 2 корня

x1,2=(-b±√D)/2a = (-(-5)±√49)/2*3 = (5±7)/6;

x1= (5-7)/6 = -2/6 = -1/3;

x2= (5±7)/6=12/6 = 2.

Пределы интегрирования a=-1/3;  b=2.  

**************

По формуле Ньютона-Лейбница

∫ₐᵇf(x)dx = F(x)|ₐᵇ = F(b)-F(a).  Тогда

S=∫²₋₀.₃₃₃(5х + 2)dx - ∫²₋₀.₃₃₃(3х^2}dx=14.388 - 8.0369 = 6,3511 кв. ед.

1)  ∫²₋₀.₃₃₃(5х + 2)dx = ∫²₋₀.₃₃₃(5x)dx + ∫²₋₀.₃₃₃(2)dx =

= 5/2(x²)|²₋₀.₃₃₃ + 2(x)|²₋₀.₃₃₃= = 5/2(2²-(-0.333)²) + 2(2-(-0.333)) =

=5/2(4-0.110889) + 2*2.333 = (5/2) * 3.889+4.666 =

=  9.7225 + 4.666 = 14.388 кв.ед.

2)  ∫²₋₀.₃₃₃(3х^2}dx = 3/3(x³)|²₋₀.₃₃₃ = (2³ - (-0.333)³) =

=  8+0.0369=  8.0369 кв. ед.

Answer 2

Відповідь:     6 19/54 кв. од.

Пояснення:

    Знайдемо точки перетину графіків даних функцій . Абсциси

    точок дадуть межі інтегрування :

    { у = 3х² ;

    { у = 5х + 2 ;       3x² = 5x + 2 ;  

                               3x² - 5x - 2 = 0 ;   D = 49 > 0 ;  x₁ = - 1/3 ;  x₂ = 2 .    

    Таким чином ,     a = - 1/3 ;      b = 2 .  Площа даної фігури

    S = ∫₋₁₎₃ ² ( 5x + 2 - 3x² )dx = ( 5 * x²/2 + 2x - 3 * x³/3 )│₋₁₎₃ ² = ( 2,5x² +

+ 2x - x³ )│₋₁₎₃ ² = ( 2,5 * 2² + 2 * 2 - 2³ ) - ( 2,5 * (- 1/3 )² - 2 * 1/3 - (- 1/3)³ ) =

= 6 - ( - 19/54 ) = 6 19/54 ( кв. од. ) ;        S =  6 19/54 кв. од.