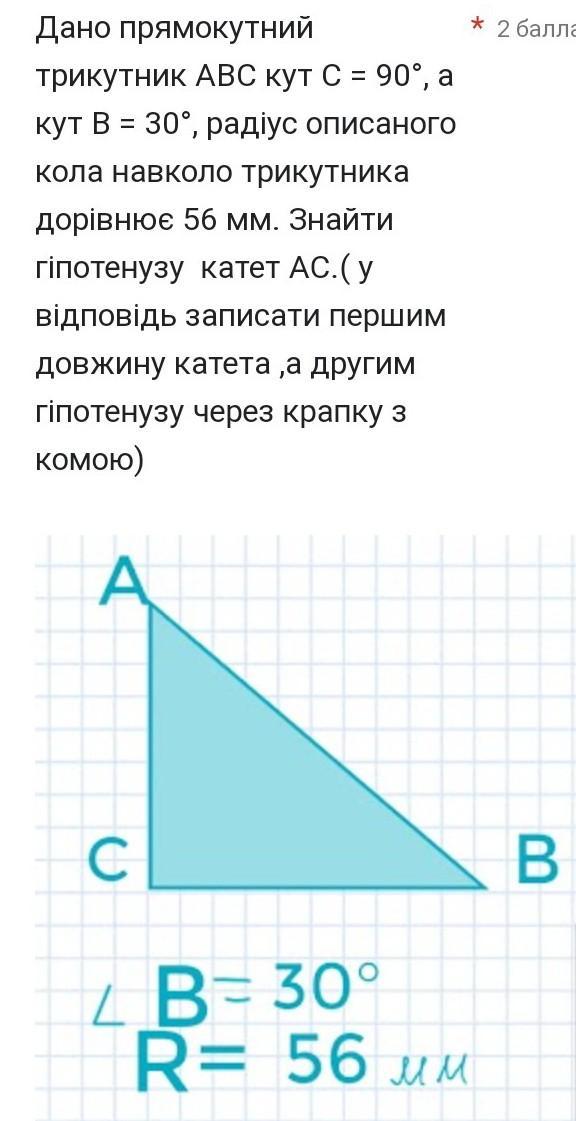
Дано прямокутний трикутник ABC кут C = 90°, а кут B = 30°, радіус описаноГО кола навколо трикутника дорівнює 56 мм. Знайти гіпотенузу катет АС.(у відповідь записати першим довжину катета,а другим гіпотенузу через крапку з комою) * 2 балла
Ответы
Розв'язання з поясненнями:
У прямокутному трикутнику ABC з кутом C = 90° та кутом B = 30°, радіус описаного кола дорівнює 56 мм.
Загальною властивістю прямокутного трикутника є теорема Піфагора, яка стверджує, що квадрат гіпотенузи (найбільшої сторони) дорівнює сумі квадратів катетів (двох менших сторін).
Знайдемо спочатку довжину катета АС. Оскільки кут B = 30°, ми знаємо, що кут A = 90° - 30° = 60°.
Так як радіус описаного кола дорівнює 56 мм, то діаметр (який відповідає гіпотенузі) дорівнює 2 * 56 мм = 112 мм.
Застосуємо теорему Піфагора:
AC^2 = AB^2 + BC^2
Для нашого трикутника:
AC^2 = (BC)^2 + (AB)^2
AC^2 = (AB)^2 + (AB/2)^2 (так як кут A = 60°, тому трикутник ABC є рівностороннім)
AC^2 = (AB)^2 + (AB^2/4)
AC^2 = (5AB^2)/4
Знаходимо співвідношення між гіпотенузою AC та катетом AB:
AC^2 = (5AB^2)/4
AB^2 = (4AC^2)/5
AВ = √[(4AC^2)/5]
AB = (2AC)/√5
Тепер знаходимо значення гіпотенузи AC:
112^2 = (2AC)^2/5
12544 = 4AC^2/5
5 * 12544 = 4AC^2
62720 = 4AC^2
AC^2 = 62720/4
AC^2 = 15680
AC = √15680
AC ≈ 125.3 мм
Таким чином, довжина катета АС дорівнює 125.3 мм, а гіпотенуза АВ дорівнює 112 мм.
Доповнення:
Якщо у вас залишилися питання, ви потребуєте рознишерене пояснення і хочете це запитати, питайте в Коментарі, постараюся відповісти швидко. Нехай щастить у виконанні задач!
Р.S:Сподіваюся, я заслуговую на найкращу відповідь?)