Question

Дискретная математика.

На ленте машины Тьюринга в четырех подряд идущих клетках записаны четыре различные буквы: A,B,C,D в произвольном порядке. Построить машину Тьюринга, меняющую местами первую и последнюю буквы. Начальное положение – стандартное.

Answer 1

Машина Тьюринга работает пошагово. На каждом шаге на основе текущего состояния и текущего просматриваемого символа определяется:

1) какой символ записать в текущую просматриваемую позицию (возможно тот же самый, что и сейчас, тогда фактически ничего не изменится);

2) как сместить каретку для просмотра очередного символа: влево, вправо или оставаться на месте;

3) в какое состояние нужно перейти (возможно в то же самое, в котором находимся сейчас, тогда фактически состояние не изменится).

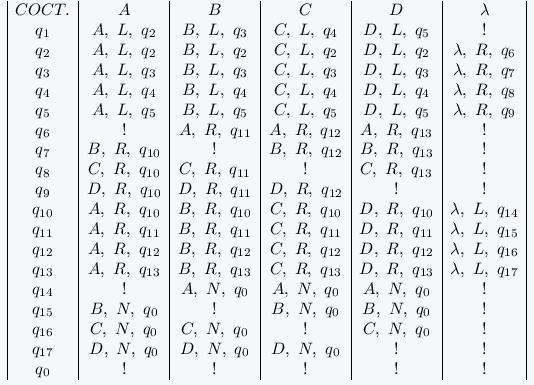
Составим алгоритм для решения задачи.

1) Поскольку по условию начальное положение - стандартное, то в начальном состоянии $q_1$ мы просматриваем крайний правый символ (справа от него находятся пустые символы, пустой символ будем обозначать λ).

Нам необходимо каким-то образом запомнить данный символ, чтобы в дальнейшем, когда мы окажемся над первым символом, мы смогли бы воспроизвести последний. В данном случае мы можем оперировать лишь состояниями машины. Таким образом, в зависимости от того, какой символ стоит последним, мы выберем одно из четырех новых состояний и перейдем в него. В любом случае изменять символы пока не нужно, а смещать каретку всегда нужно влево.

$\begin{array}{|c|c|c|c|c|c|}COCT.&A&B&C&D&\lambda\\q_1&A,\ L,\ q_2&B,\ L,\ q_3&C,\ L,\ q_4&D,\ L,\ q_5&!\end{array}$

Инструкция машине состоит из перечисленных через запятую:

- нового символа в просматриваемой ячейке;

- команды смещения каретки (L - влево, R - вправо, N - оставаться на месте);

- нового состояния.

Так если в состоянии $q_1$ в просматриваемой ячейке находится буква А, то будет выполнена инструкция $(A,\ L,\ q_2)$, а именно в просматриваемую ячейку будет записана буква А (фактически ничего не изменится, ведь там уже находится буква А), каретка будет смещена влево, а машина перейдет в состояние $q_2$.

Для пустого символа λ вместо инструкции прописана команда остановки (!), поскольку по условию в начальном положении просматриваемый символ непустой, а выйдя из состояния $q_1$ возвращаться в него мы не планируем.

2) Для любого из полученных состояний мы должны продолжать двигаться налево, не изменяя символы и состояния, до тех пор, пока просматриваемый символ не окажется пустым. Если просматриваемый символ - пустой, то первый символ находится справа от нас, и нам необходимо сместиться вправо и поменять состояние, причем каждому из четырех ранее созданных состояний будет соответствовать свое новое состояние.

$\begin{array}{|c|c|c|c|c|c|}COCT.&A&B&C&D&\lambda\\q_2&A,\ L,\ q_2&B,\ L,\ q_2&C,\ L,\ q_2&D,\ L,\ q_2&\lambda,\ R,\ q_6\\q_3&A,\ L,\ q_3&B,\ L,\ q_3&C,\ L,\ q_3&D,\ L,\ q_3&\lambda,\ R,\ q_7\\q_4&A,\ L,\ q_4&B,\ L,\ q_4&C,\ L,\ q_4&D,\ L,\ q_4&\lambda,\ R,\ q_8\\q_5&A,\ L,\ q_5&B,\ L,\ q_5&C,\ L,\ q_5&D,\ L,\ q_5&\lambda,\ R,\ q_9\end{array}$

3) Находясь над первой ячейкой мы записываем значение последнего символа, ориентируясь на состояние машины. В зависимости от значения текущего просматриваемого символа, мы осуществляем переход в одно из четырех новых состояний. Смещение каретки должно выполняться вправо.

$\begin{array}{|c|c|c|c|c|c|}COCT.&A&B&C&D&\lambda\\q_6&!&A,\ R,\ q_{11}&A,\ R,\ q_{12}&A,\ R,\ q_{13}&!\\q_7&B,\ R,\ q_{10}&!&B,\ R,\ q_{12}&B,\ R,\ q_{13}&!\\q_8&C,\ R,\ q_{10}&C,\ R,\ q_{11}&!&C,\ R,\ q_{13}&!\\q_9&D,\ R,\ q_{10}&D,\ R,\ q_{11}&D,\ R,\ q_{12}&!&!\end{array}$

Команды остановки прописаны для пустого просматриваемого символа, которого не может быть в ситуации, когда мы просматриваем первый символ, а также для ситуаций, когда первый символ заведомо не может принимать определенное значение. Например, состояние $q_6$ несет в себе информацию о том, что последним символом была буква А, а значит первый символ не может быть буквой А.

4) По аналогии с пунктом 2) мы двигаемся вправо до тех пор, пока просматриваемый символ непустой. Когда просматриваемый символ оказывается пустым, мы меняем состояние и смещаемся влево, таким образом, оказываясь над последним символом.

$\begin{array}{|c|c|c|c|c|c|} COCT. & A & B & C & D & \lambda \\ q_{10} & A,\ R,\ q_{10} & B,\ R,\ q_{10} & C,\ R,\ q_{10} & D,\ R,\ q_{10} & \lambda,\ L,\ q_{14} \\q_{11} & A,\ R,\ q_{11} & B,\ R,\ q_{11} & C,\ R,\ q_{11} & D,\ R,\ q_{11} & \lambda,\ L,\ q_{15} \\q_{12} & A,\ R,\ q_{12} & B,\ R,\ q_{12} & C,\ R,\ q_{12} & D,\ R,\ q_{12} & \lambda,\ L,\ q_{16} \\q_{13} & A,\ R,\ q_{13} & B,\ R,\ q_{13} & C,\ R,\ q_{13} & D,\ R,\ q_{13} & \lambda,\ L,\ q_{17} \end{array}$

5) Ориентируясь по состоянию машины, мы записываем значение первого символа в последнюю ячейку, после чего переходим в заключительное состояние, в котором выполнение алгоритма завершается.

$\begin{array}{|c|c|c|c|c|c|} COCT. & A & B & C & D & \lambda \\ q_{14} & ! & A,\ N,\ q_0 & A,\ N,\ q_0 & A,\ N,\ q_0 & ! \\q_{15} & B,\ N,\ q_0 & ! & B,\ N,\ q_0 & B,\ N,\ q_0 & ! \\q_{16} & C,\ N,\ q_0 & C,\ N,\ q_0 & ! & C,\ N,\ q_0 & ! \\q_{17} & D,\ N,\ q_0 & D,\ N,\ q_0 & D,\ N,\ q_0 & ! & ! \\q_0 & ! & ! & ! & ! & !\end{array}$