Предмет: Математика,
автор: everythings1590
ОЧЕНЬ СРОЧНО!!!! ДАМ 50 БАЛЛОВ!!!!
Обчислити значення похідної функції y=(2x²-1)In²x у точці Xo=1
Ответы
Автор ответа:
0
Ответ:
Найти производную произведения двух функций .
Формула : .
Приложения:
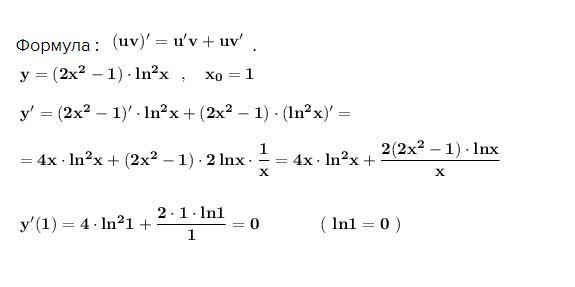
Похожие вопросы
Предмет: Математика,
автор: rayabulatkina
Предмет: Алгебра,
автор: koliastanev11
Предмет: Химия,
автор: usikivan31
Предмет: Математика,
автор: polina35535
Предмет: Математика,
автор: thedenplayden