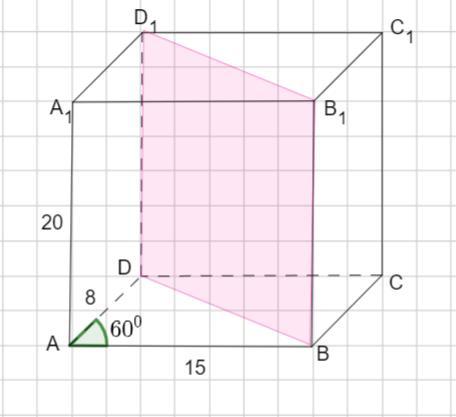
Основою прямої призми є паралелограм зі сторонами 8 і 15 та гострим кутом 60°. Висота призми дорівнює 20. Визначте площу меншого діагонального перерізу призми.
d²=8²+15² - 2•8•15• cos 60°
d=13
S=d•h, S=13•20
Ответы
Ответ:
260 кв. ед.
Пошаговое объяснение:
Основанием прямой призмы является параллелограмм со сторонами 8 и 15 и острым углом 60°. Определить площадь меньшего диагонального сечения.
Пусть дана прямая призма .
ABCD - параллелограмм.
АВ =15 ед. , АD = 8 ед. ∠А = 60°. Тогда диагональ ВD - наименьшая диагональ параллелограмма и прямоугольник - наименьшее диагональное сечение.
Чтобы найти площадь прямоугольника, надо длину умножить на ширину.
высота призмы
Найдем диагональ ВD из Δ АВD по теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
BD² = AB² +AD² - 2· AB ·AD ·cos A;
BD² = 15² +8² - 2· 15 ·8 ·cos 60° = 225 +64 - 2· 120 ·0,5 = 289 - 120 = 169;
BD = √169 = 13 ед.
Тогда найдем площадь наименьшего диагонального сечения
кв. ед.
#SPJ1