Поможіть з ВишМатом, даю багато балів
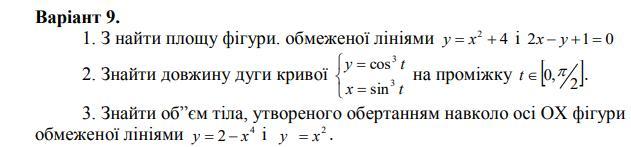
Ответы
1. Щоб знайти площу фігури, обмеженої лініями у = х^2+4 і 2х - у + 1 = 0, спочатку потрібно знайти точки їх перетину.
Співставимо обидві рівняння:
х^2 + 4 = 2х - у + 1
Перепишемо друге рівняння у виразі у:
у = 2х + 1
Підставимо це значення у перше рівняння:
х^2 + 4 = 2х - (2х + 1) + 1
Спростимо вираз:
х^2 + 4 = 2х - 2х - 1 + 1
х^2 + 4 = 0
Розв'яжемо це квадратне рівняння:
х^2 = -4
Так як квадрат від'ємного числа не має розв'язків у дійсних числах, то фігура обмежена цими лініями немає перетину та площі.
3.Щоб знайти об'єм тіла, утвореного обертанням фігури обмеженої лініями у = 2 - x^4 і у = x^2 навколо осі OX, ми можемо використати формулу об'єму оберненої фігури.
Об'єм тіла, утвореного обертанням навколо осі OX, можна обчислити за формулою:
V = ∫[a,b]π(R(x)^2 - r(x)^2)dx
де a та b - інтервал, на якому обмежена фігура, R(x) - радіус зовнішньої кривої, r(x) - радіус внутрішньої кривої.
За заданими лініями, знайдемо точки їх перетину:
2 - x^4 = x^2
x^4 + x^2 - 2 = 0
(x^2 - 1)(x^2 + 2) = 0
Звідси отримуємо два значення x: x = 1 та x = -1.
Таким чином, інтервал, на якому обмежена фігура, буде [-1, 1].
Знайдемо радіуси зовнішньої та внутрішньої кривих:
R(x) = 2 - x^4
r(x) = x^2
Т
епер можемо обчислити об'єм:
V = ∫[-1,1]π((2 - x^4)^2 - (x^2)^2)dx
Це інтеграл, який можна обчислити числовими методами або використовувати програмне забезпечення для символьних обчислень, таке як символьний математичний пакет.
Надіюся, ця інформація була корисною. Якщо у вас є будь-які інші питання, будь ласка, звертайтеся!