Предмет: Алгебра,
автор: petdrobyka
Розв`язати диференційне рівняння!
Приложения:
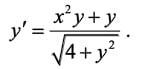
Ответы
Автор ответа:
0
Ответ:
Решить дифференциальное уравнение .
Вычислим отдельно интеграл, стоящий в левой части равенства с помощью замены .
Вычислим отдельно интеграл, стоящий в правой части равенства .
Похожие вопросы