Question

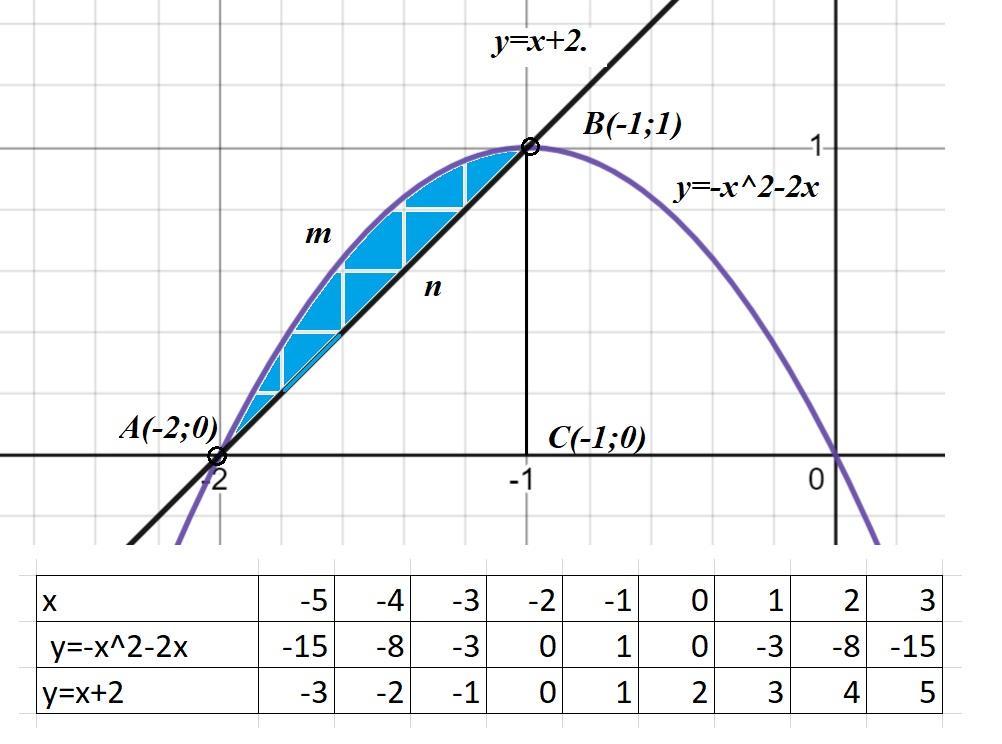
Вычислите площадь фигуры ограниченной линиями у=-х^2-2х и у=х+2

Answer 1

Ответ:      1/6 кв.ед.

Объяснение:

Строим графики функций    у=-х^2-2х;  у=х+2.  (См. скриншот)

S=s(AmBC) - s(AnBC);

Площадь s=∫ₐᵇf(x)dx.

Пределы интегрирования

-х^2-2х=х+2;

x1=a= -2;   x2=b= -1.  Тогда

S=∫₋₂⁻¹ (-х^2-2х)dx - ∫₋₂⁻¹(х+2)dx = 2/3 - 0,5 = 1/6 кв.ед.

1)  ∫₋₂⁻¹ (-х^2-2х)dx = -∫₋₂⁻¹(x²)dx - 2∫₋₂⁻¹(x)dx = -1/3(x³)|₋₂⁻¹-2/2(x²)|₋₂⁻¹ =

= -1/3((-1)³ - (-2)³)  - ((-1)²-(-2)²) = -1/3(-1+8) - (1-4) =

=  -1/3*(7) - (-3) = -7/3+3 = 2/3 кв. ед.

2)  ∫₋₂⁻¹(х+2)dx = ∫₋₂⁻¹(x)dx + 2∫₋₂⁻¹dx = 1/2(x²)|₋₂⁻¹ + 2(x)|₋₂⁻¹ =

= 1/2((-1)²-(-2)²) +2(-1-(-2)) = 1/2(1-4) +2(-1+2) = -3/2 + 2 = 0.5 кв.ед.