Предмет: Геометрия,
автор: Bobik23598
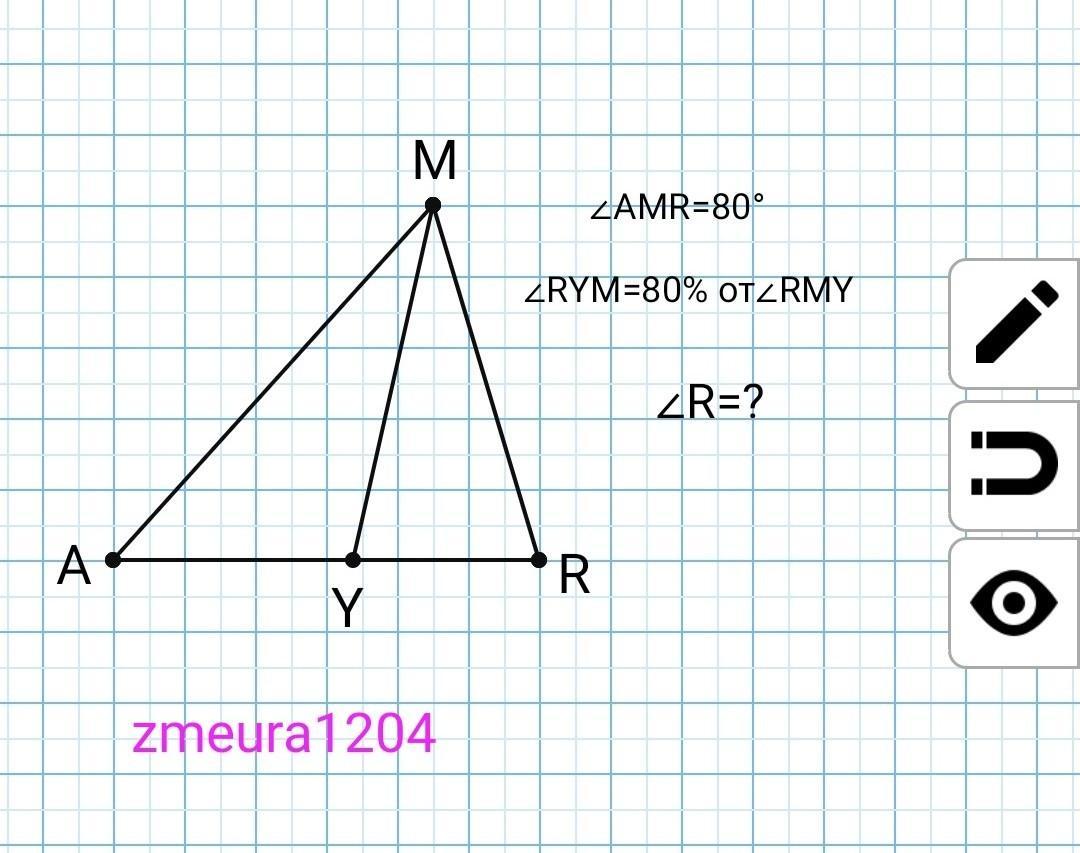
В треугольнике ARM проведена биссектриса MY. Найдите угол ARM, если RMA=80 градусов ; RYM cоставляет 80 % от угла RMY, а сумма углов треугольника RMY равна 180 градусов
Bobik23598:
но это последний вопрос
данное условие задачи не правильно составлено. Я напишу ответ, а вы посмотрите. Но решение неправильно.
а что именно не правильно?
Если угол R=108°, то ∠АМR=80°; сумма углов в треугольнике АМR, не будет 180°; (108+80°+∠А)
Процент должен быть другой, или от другого угла.
Не знаю что не правильно, но я ввел ваш ответ и мне засчитало как правильно, спасибо большое:), я ваш должник
Неправильно условие задачи.
Сумма углов любого треугольника 180°; Посчитайте сумму углов ∆АМR.
∠M=80°; ∠R=108°; ....и ещё один угол есть ∠А...
Да , ошибка условия.
Ответы
Автор ответа:
1
Ответ:
Условие задачи не правильно составлено.
∠АRM=108°
Объяснение:
∠AMY=∠RMY, МY- биссектриса.
∠RMY=∠AMR/2=80°/2=40°
Пропорция:
100%- 40°. (100%- ∠RMY)
80%- x°. (80%- ∠RYM)
x=80*40/100=32° ∠RYM
Сумма углов в треугольнике равна 180°
∠R=180°-∠RMY-∠RYM=
=180°-40°-32°=108°
Приложения:
Автор ответа:
0
Если угол RMA=80°, то биссектриса МY поделила этот угол на равные части—>
Угол YMR = углу YMA =40°
Угол RYM=80% от угла RMY—>
100% это угол RMY; 100%=40°
40°/100%=0,4° это 1%
Угол RYM=80%*0,4°=32°
Треугольник RMY=180°, угол RYM=32°, угол RMY=40°, угол ARM-?
Угол ARM=180-40-32=108°
Ответ:108°
Угол YMR = углу YMA =40°
Угол RYM=80% от угла RMY—>
100% это угол RMY; 100%=40°
40°/100%=0,4° это 1%
Угол RYM=80%*0,4°=32°
Треугольник RMY=180°, угол RYM=32°, угол RMY=40°, угол ARM-?
Угол ARM=180-40-32=108°
Ответ:108°
Похожие вопросы
Предмет: География,
автор: Ferinskaairina
Предмет: Математика,
автор: dipoplavsk
Предмет: История,
автор: tanicheva25112007
Предмет: Математика,
автор: nikitavalkov56
Предмет: Алгебра,
автор: ltloiaia