Предмет: Геометрия,
автор: shebysho
Кут між висотами паралелограма проведеними з вершини тупого кута 60° знайти площу паралелограма якщо його сторони дорівнюють 4 см і 16 см
Даю 200 балів
Ответы
Автор ответа:
0
Ответ:
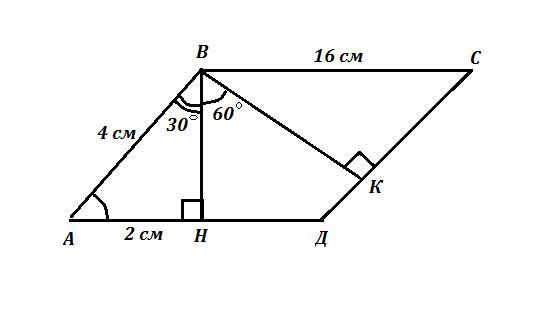
Параллелограмм АВСД . Высоты параллелограмма АН и АК ,
ВН ⊥ АД , ВК ⊥ СД . ∠НВК=60° , АВ=4 см , АД=16 см . Найти S .
Рассмотрим четырёхугольник НВКД . Сумма его внутренних углов равна 360° , а ∠ВНД+∠ВКД=90°+90°=180° .
Тогда ∠НВК+∠НДК = 360°-(∠ВНД+∠ВКД) = 360°-180° = 180° .
И тупой угол ∠НДК = 180°-60° = 120° .
Тупой угол параллелограмма равен 120° , значит его острый угол
∠А=180°-120°=60°
Рассмотрим ΔАВН - прямоугольный , ∠АВН=90°-∠А = 90°-60°=30° ,
АВ=4 см .
Против угла в 30° лежит катет, равный половине гипотенузы , значит АН=АВ : 2 =4 : 2 =2 (см)
Катет ВН =√(АВ²-АН²)=√(4²-2²)=√12=2√3 (см) .
Но ВН - высота параллелограмма , значит его площадь равна
S= АД * ВН = 16 * 2√3 = 32√3 (см²)
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: gofurjonovahborbek
Предмет: Українська література,
автор: svetlananekolenko
Предмет: Алгебра,
автор: helloween13euwi
Предмет: Физика,
автор: proigrok2281
Предмет: Литература,
автор: vladis41969