Предмет: Алгебра,
автор: egor3665
17. Решите уравнение
Приложения:
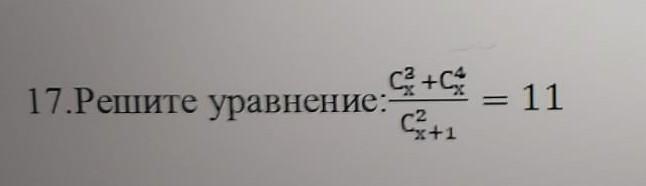
Ответы
Автор ответа:
0
Ответ: x=13.
Объяснение:
Похожие вопросы
Предмет: Физика,
автор: nikitayutub
Предмет: История,
автор: angelinayatsenk05
Предмет: Українська мова,
автор: ivanTV3090
Предмет: Геометрия,
автор: f89535244420
Предмет: Алгебра,
автор: mileschannel1337