Предмет: Геометрия,
автор: nastabeletckaa
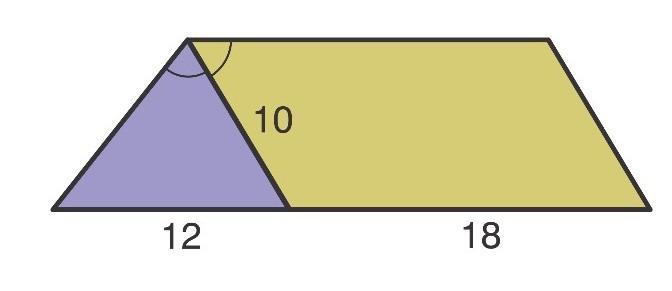
Бісектриса одного з кутів трапеції ділить трапецію на паралелограм і трикутник. За даними креслення обчисліть периметр трапеції.
Приложения:
Ответы
Автор ответа:
0
Оскільки бісектриса трапеції ділить її на паралелограм і трикутник, то можна побудувати допоміжну лінію, яка була б бісектрисою другого кута трапеції і перетинала б паралелограм у його середині. Позначимо цю точку серединою М.

Так як АМ є бісектрисою кута А, то вона перпендикулярна до ВС. Отже, АМ є висотою трикутника АВС і ділить його на дві рівні частини. Так як трикутник АВС є рівнобедреним, то точка М є серединою сторони АВ.
Також за умовою задачі сторона ВС паралельна стороні АD, тому кути А и С є взаємно доповнювальними. Отже, кут ВМС дорівнює куту АМВ і також є прямим.
Так як ВМ=МС, то паралелограм ВМС є ромбом. Оскільки сторона АВ ділить ромб на два рівні трикутники, то можна знайти довжину сторони ВС:
$$BC = 2 \cdot BM = 2 \cdot \frac{AV}{2} = AV = 4 \text{ см}$$
Також можна знайти довжину сторони АD:
$$AD = AB - BD = 8 \text{ см} - 3 \text{ см} = 5 \text{ см}$$
Отже, периметр трапеції АВСD дорівнює:
$$P = AB + BC + CD + AD = 8 \text{ см} + 4 \text{ см} + 6 \text{ см} + 5 \text{ см} = 23 \text{ см}$$
Відповідь: периметр трапеції дорівнює 23 см.

Так як АМ є бісектрисою кута А, то вона перпендикулярна до ВС. Отже, АМ є висотою трикутника АВС і ділить його на дві рівні частини. Так як трикутник АВС є рівнобедреним, то точка М є серединою сторони АВ.
Також за умовою задачі сторона ВС паралельна стороні АD, тому кути А и С є взаємно доповнювальними. Отже, кут ВМС дорівнює куту АМВ і також є прямим.
Так як ВМ=МС, то паралелограм ВМС є ромбом. Оскільки сторона АВ ділить ромб на два рівні трикутники, то можна знайти довжину сторони ВС:
$$BC = 2 \cdot BM = 2 \cdot \frac{AV}{2} = AV = 4 \text{ см}$$
Також можна знайти довжину сторони АD:
$$AD = AB - BD = 8 \text{ см} - 3 \text{ см} = 5 \text{ см}$$
Отже, периметр трапеції АВСD дорівнює:
$$P = AB + BC + CD + AD = 8 \text{ см} + 4 \text{ см} + 6 \text{ см} + 5 \text{ см} = 23 \text{ см}$$
Відповідь: периметр трапеції дорівнює 23 см.
Похожие вопросы
Предмет: Українська література,
автор: Helloo086
Предмет: Українська мова,
автор: sofiakl277
Предмет: Английский язык,
автор: gannadeznuk714
Предмет: Алгебра,
автор: oknesnde