Предмет: Алгебра,
автор: Thgc
70 балів! Спростити вираз!!! ПОТРІБНО НЕГАЙНО!!!
Приложения:
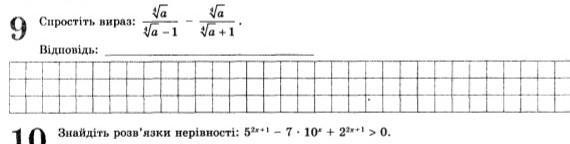
Ответы
Автор ответа:
0
10)
Автор ответа:
1
Ответ:
ответ смотри на фотографии, дай пожалуйста корону
Приложения:
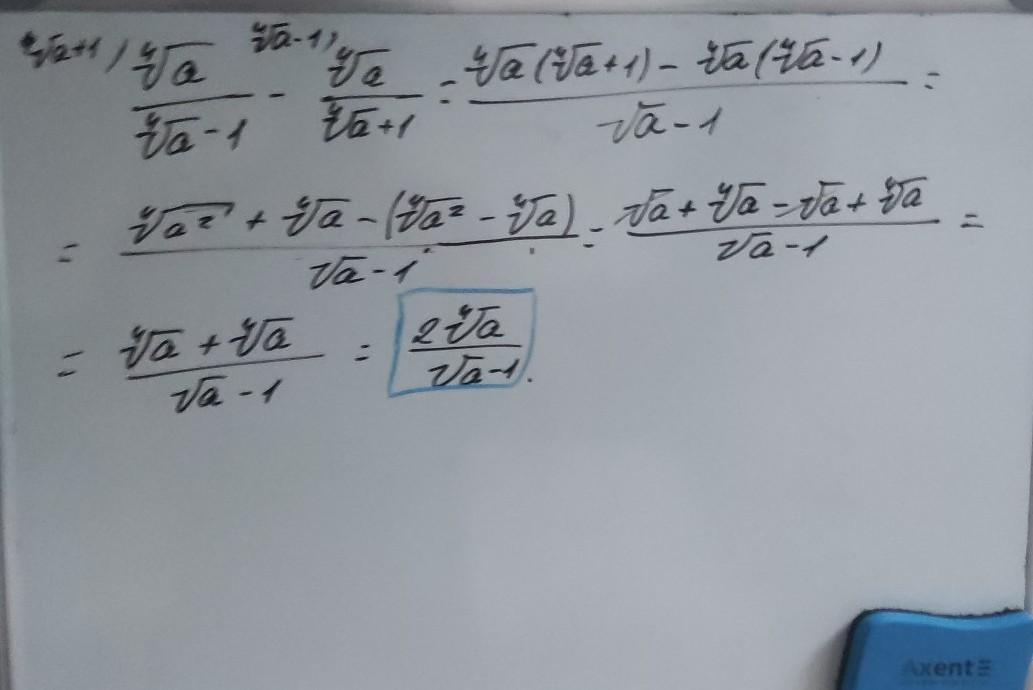
Похожие вопросы
Предмет: Українська мова,
автор: 2012mmaaxx
Предмет: Геометрия,
автор: daniilcaruk651
Предмет: Математика,
автор: alinashvets2009
Предмет: Математика,
автор: drakosha03080484
Предмет: Английский язык,
автор: emilfatkhullin2017