РЕБЯТА, РЕШИТ МОЮ
ЖИЗНЬ!!
Шар пересечен плоскостью. Расстояние от центра шара до плоскости сечения равно 4 см. Найдите площадь поверхности шара, обьем шара, площадь сечения, если радиус сечения равен
3 сМ.
Ответы
Ответ:
S (шара) = 100π см²
V(шара) = 500π/3 см³
S (сеч) = 9π см²
Пошаговое объяснение:
Шар пересечен плоскостью. Расстояние от центра шара до плоскости сечения равно 4 см. Найдите площадь поверхности шара, обьем шара, площадь сечения, если радиус сечения равен 3 см.
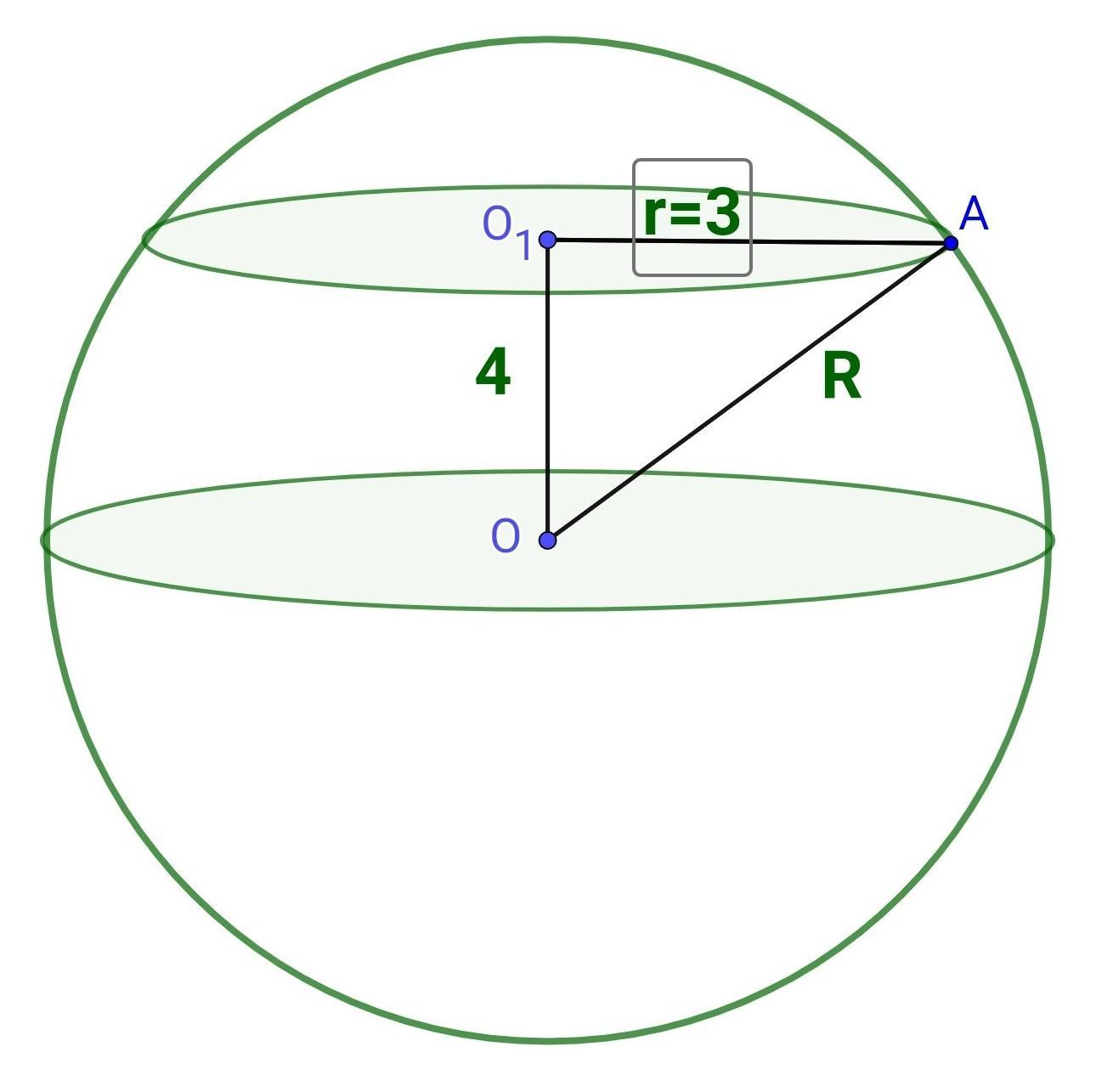
Сечение шара - круг радиусом r = 3 см. Центр сечения - точка О₁, которая является основой перпендикуляра, опущенного с центра шара - точки О на площадь сечения. ОО₁ = 4 см.
Радиус шара ОА.
По теореме Пифагора из прямоугольного треугольника ОО₁А найдём радиус шара ОA:
R² =OA²=OO₁²+O₁A²=4²+3²=16+9= 25
R = 5 см
Площадь поверхности шара найдём по формуле:
S = 4πR²
S(шара) = 4π•25 = 100π (см²)
Объем шара находим по формуле:
(см³)
Площадь сечения (круга) находим по формуле:
S = πR²
S(сеч) = π • 3² = 9π (см²)
#SPJ1