Предмет: Математика,
автор: markfrost825
Обчислити площу фігури, обмеженої лініями: y=2+x2, y=4+x
Ответы
Автор ответа:
0
Ответ: 4.5 кв. ед.
Пошаговое объяснение:
S=∫ₐᵇf(x)dx.
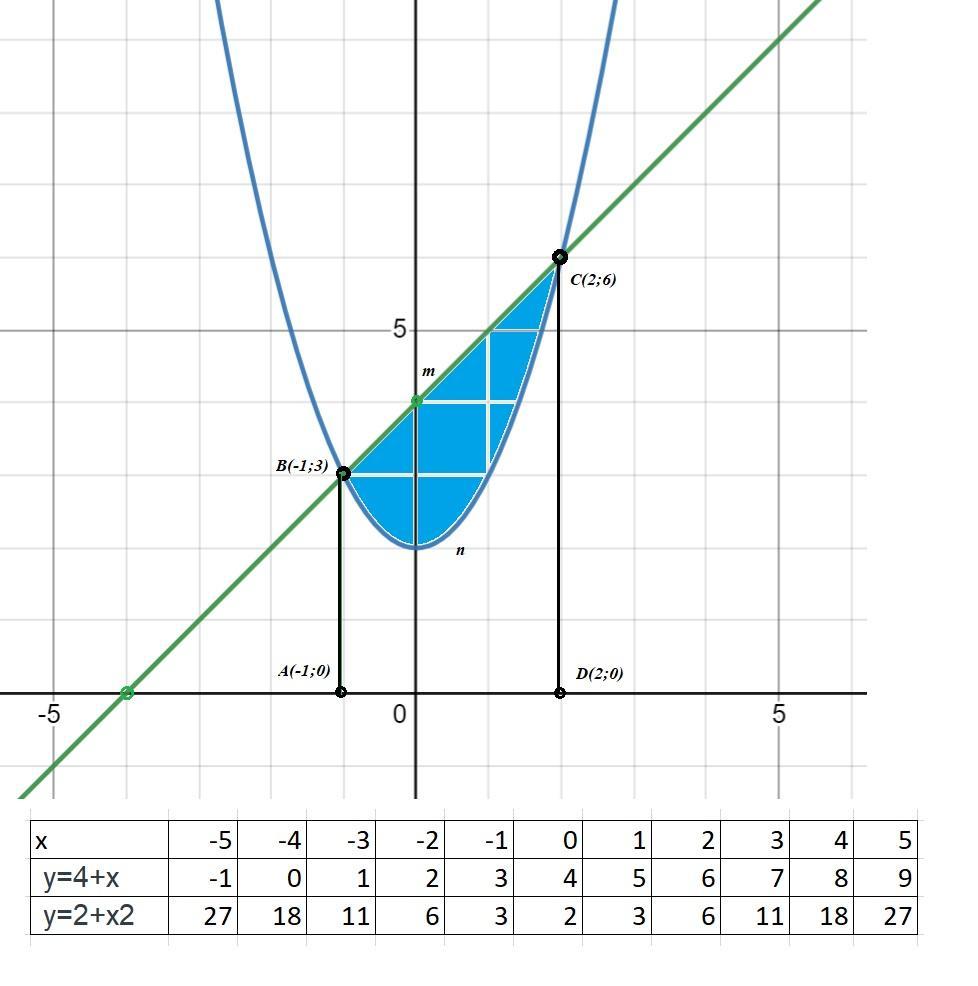
Строим графики функций y=2+x^2; y=4+x. (См скриншот)
S=S(ABmCD) - S(ABnCD).
Пределы интегрирования a=-1; b=2.
S=∫₋₁²(4+x)dx - ∫₋₁²(2+x^2)dx = 13.5-9=4.5 кв. ед.
По формуле Ньютона-Лейбница
1) ∫₋₁²(4+x)dx = ∫₋₁²4dx+ ∫₋₁²xdx = 4(x)|₋₁² + (x^2/2)|∫₋₁² =
= 4(2-(-1)) + 1/2(2^2-(-1)^2) = 4*3 + 1/2(3) = 12+1.5 = 13.5.
2) ∫₋₁²(2+x^2)dx = 2∫₋₁²dx + ∫₋₁²x^2dx = 2(x)|₋₁² + 1/3(x^3)|₋₁² =
= 2(2-(-1)) + 1/3(2^3-(-1)^3) = 2*3 +1/3(8-(-1)) = 6+9/3 = 6+3= 9.
Приложения:
ildar502020:
Якщо питань немає, виберіть кількість зірочок і оцініть відповідь.
Thank You!
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ph4crj4bjv
Предмет: Українська мова,
автор: Licicka
Предмет: История,
автор: Sofia7777777777777
Предмет: Русский язык,
автор: allssan