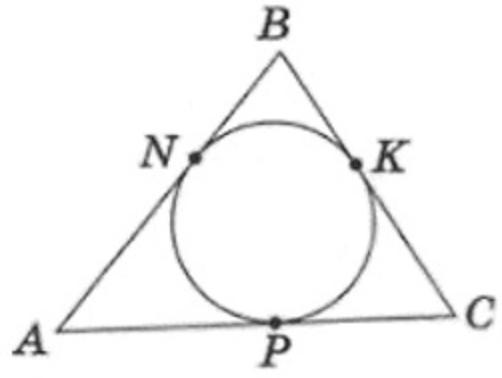
Трикутник, описано навколо кола (див. малюнок), точки
N. K i P - точки дотику. АС = 12 см, ВК = 4 см. Знайдіть периметр
трикутника ABC.
Будьласка допоможіть!!!!
Ответы
Щоб знайти периметр трикутника АВС, нам потрібно знайти довжини всіх його сторін.
Оскільки трикутник описаний навколо кола, точка К є точкою дотику кола до сторони АВ. За теоремою про дотичну до кола, дотична, проведена до кола, є перпендикулярною до радіуса, що його перетинає. Тому сторона АК є перпендикулярною до сторони ВК, і ми можемо використати цю властивість для знаходження довжини сторони АК.
За теоремою Піфагора, ми можемо записати:
АС² = АК² + КС²,
де АС = 12 см (за умовою), КС = ВК = 4 см (за умовою). Замінюючи відомі значення, отримуємо:
12² = АК² + 4².
144 = АК² + 16.
АК² = 144 - 16.
АК² = 128.
АК = √128.
АК = 8√2.
Тепер, коли ми знаємо довжину сторони АК, можемо знайти довжини сторін АС і СВ. Оскільки АК є перпендикулярною до сторони АВ, ми можемо поділити сторону АВ на дві частини, АК і КВ, і використати пропорцію між довжинами сторін трикутника:
АС/АК = АВ/КВ.
Підставляючи відомі значення, отримуємо:
12/8√2 = АВ/4.
Знаходячи АВ, отримуємо:
АВ = (12/8√2) * 4.
АВ = 3√2 * 4.
АВ = 12√2.
Тепер ми можемо знайти периметр трикутника АВС, склавши довжини всіх його сторін:
Периметр = АВ + АК + КС.
Периметр = 12√2 + 8√2 + 4.
Периметр = 20√2 + 4.
Отже, периметр трикутника АВС дорівнює 20√2 + 4.