Question

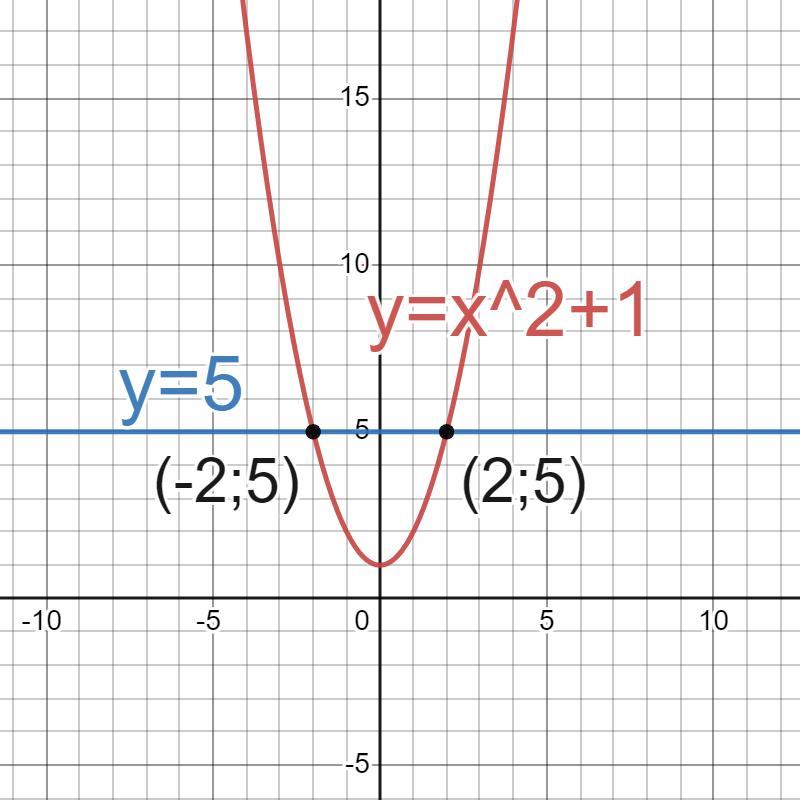
Обчисліть площу фігури, обмеженої лініями. Зробити малюнок Y = X^2+1 i y=5.

Дуже довго мучилась над цією задачею, але відповідь в мене все одно однакова 0 ..

Answer 1

Пояснення:

y=x²+1        y=5            S=?

$x^2+1=5\\\\x^2-4=0\\\\(x+2)*(x-2)=0\\\\x_1=-2\ \ \ \ \ x_2=2.$

$\displaystyle\\S=\int\limits^2_{-2} {(5-(x^2+1))} \, dx=\int\limits^2_{-2} {(5-x^2-1)} \, dx =\int\limits^2_{-2} {(4-x^2)} \, dx=\\\\\\ =(4x-\frac{x^3}{3} )\ |_{-2}^2=4x\ |_{-2}^2-\frac{x^3}{3} \ |_{-2}^2=4*2-4*(-2)-(\frac{2^3}{3} -\frac{(-2)^3}{3} )=\\\\\\=8-(-8)-(\frac{8}{3} -(-\frac{8}{3}))=16- \frac{16}{3}=16-5\frac{1}{3} =10\frac{2}{3} .$

Відповідь: S=10,666667 кв. од.