У Васі був дуже гарний паперовий опуклий 14-кутник, усі сторони якого були рівними. Його молодший брат знайшов ножиці і акуратно розрізав його по прямій лінії на дві частини, так що вийшло 2 багатокутники, (не обов'язково однакові), потім він взяв один з отриманих багатокутників і розрізав його по прямій лінії ще на дві частини. Так він повторював до тих пір, поки на столі не виявилось 11 багатокутників з однаковою кількістю кутів. Яка кількість кутів могла бути у кожного з цих багатокутників? Знайдіть усі рішення і доведіть, що інших немає.
Ответы
Відповідь:
багатокутники мали 4 кути
Пояснення:
У Васі був дуже гарний паперовий опуклий 14-кутник, усі сторони якого були рівними. Його молодший брат знайшов ножиці і акуратно розрізав його по прямій лінії на дві частини, так що вийшло 2 багатокутники, (не обов'язково однакові), потім він взяв один з отриманих багатокутників і розрізав його по прямій лінії ще на дві частини. Так він повторював до тих пір, поки на столі не виявилось 11 багатокутників з однаковою кількістю кутів. Яка кількість кутів могла бути у кожного з цих багатокутників? Знайдіть усі рішення і доведіть, що інших немає.
Розв'язання:
Результат розрізання опуклого 14-кутника (n₀=14) на 11 багатокутників з однаковою кількістю кутів, говорить про те, що зробили 10 розрізів (k=10) по прямій лінії і сума всіх кутів багатокутників кратна 11.
Варіанти розрізання та результат:
1) Якщо кожного разу багатокутник розрізали по діагоналі (тобто лінія розрізу проходила через вершини кутів), то сума всіх кутів утворених багатокутників (Sn), з кожним розрізом збільшувалася на 2: Sn=n₀+2*k=14+2*10=34
2) Якщо кожного разу багатокутник розрізали по лінії, яка проходить через вершину кута та протилежну сторону, то сума всіх кутів утворених багатокутників (Sn), з кожним розрізом збільшувалася на 3:
Sn=n₀+3*k=14+3*10=44
3) Якщо кожного разу багатокутник розрізали по лінії, яка проходить тільки через сторони, то сума всіх кутів утворених багатокутників (Sn), з кожним розрізом збільшувалася на 4:
Sn=n₀+4*k=14+4*10=54
4) Якщо при розрізанні використовували змішування варіантів 1-3, то сума всіх кутів утворених багатокутників 34≤Sn≤54.
У цих межах кратна 11 лише сума кутів Sn=44.
Отже, отримані в результаті 11 багатокутників мали по Sn:11=44:11=4 кути.
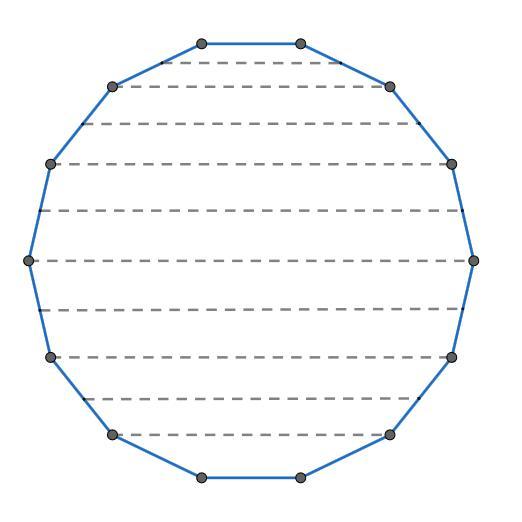
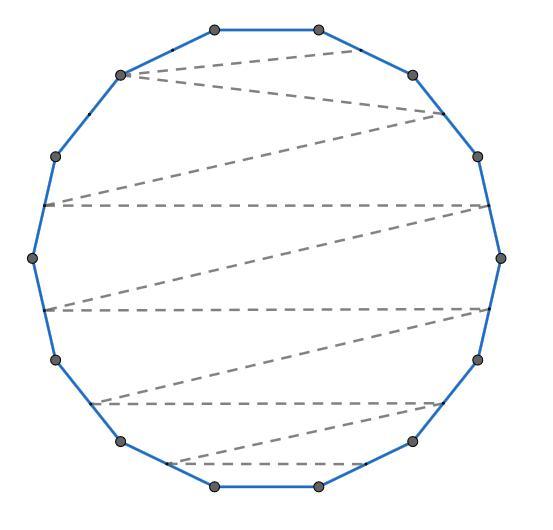
На фото 1-2 зображені можливі приклади розрізання опуклого 14-кутника на 11 чотирикутників.
#SPJ1