Question

Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і утворює з основою трапеції кут 30°. Знайдіть плошу трапеції, якщо радус кола, описаного навколо неї, дорівнює R.
З малюнком та поясненням

Answer 1

Ответ:

Площа трапеції дорівнює

$\bf \frac{3 {R}^{2} \sqrt{3} }{4}$ ед²

Объяснение:

Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і утворює з основою трапеції кут 30°. Знайдіть плошу трапеції, якщо радус кола, описаного навколо неї, дорівнює R.

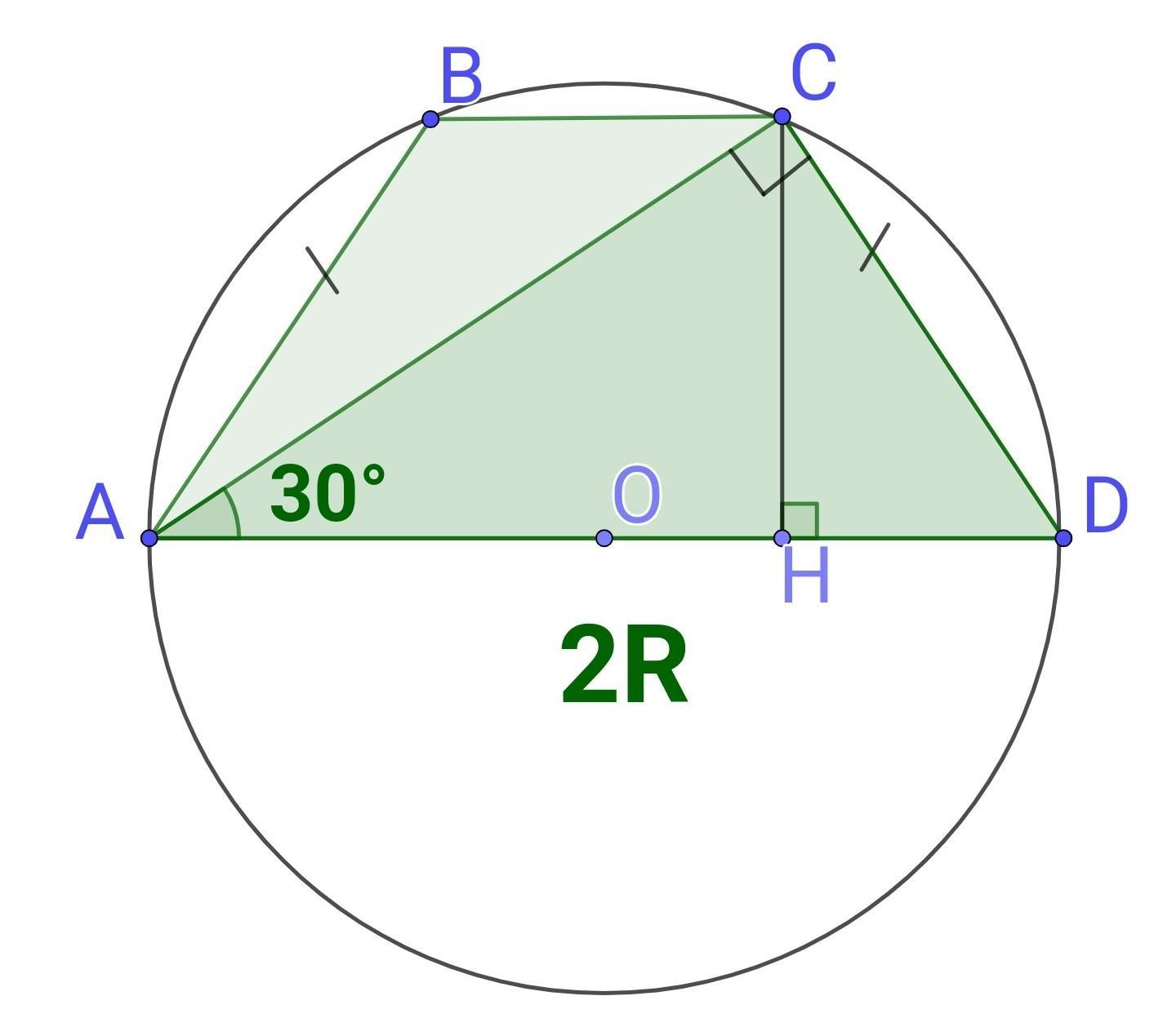
Нехай ABCD - дана трапеція. BC || AD, AB=CD. AC⟂CD, ∠CAD = 30°.

1) Так як ∠CAD є вписаним у коло і дорівнює 90°, то він спирається на діаметр. AD - діаметр кола, у яке вписано трапецію. AD=2R.

2) Проведемо висоту CH. За властивістю рівнобічної трапеції:

$\boxed {AH = \dfrac{AD + BC}{2} }$

3) З прямокутного трикутника ACD (∠C=90°) за означенням косинуса гострого кута прямокутного трикутника маємо:

$cos\angle CAD = \dfrac{AC}{AD}$

Тоді AC =AD•cos30°=2R • √3/2 = R√3

4) З прямокутного трикутника ACH (∠H=90°):

• за означенням косинуса гострого кута прямокутного трикутника:

$cos\angle CAH = \dfrac{AH}{AC}$

$AH = AC\cos30^\circ = \bf \dfrac{3R}{2}$

• за означенням синуса гострого кута прямокутного трикутника:

$sin\angle CAH = \dfrac{CH}{AC}$

$CH = AC\sin30^\circ = \bf \dfrac{R \sqrt{3} }{2}$

5) Площа трапеції:

$\boxed {\bf S = \frac{AD + BC}{2}\cdot CH}$

$S = AH\cdot CH = \dfrac{3R}{2} \cdot \dfrac{R \sqrt{3} }{2} = \bf \dfrac{3 {R}^{2} \sqrt{3} }{4}$ ед²

#SPJ1