Предмет: Алгебра,
автор: Аноним
Найти полный дифференциал z=2xysinx+3e^x+2y/x
Ответы
Автор ответа:
0
Ответ:
Полный дифференциал функции двух переменных находится по формуле
.
Приложения:
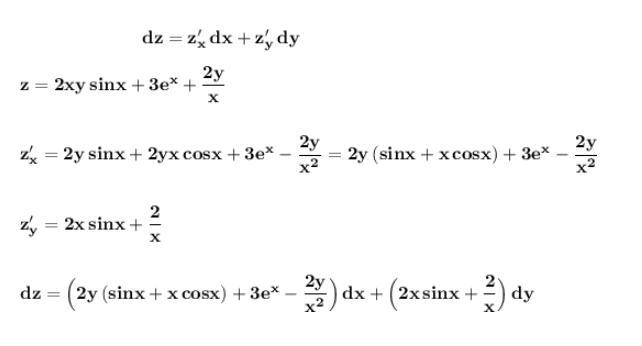
Похожие вопросы
Предмет: Другие предметы,
автор: ivancube0704
Предмет: Английский язык,
автор: kaplunchristina28
Предмет: География,
автор: melnuk22042012i
Предмет: Английский язык,
автор: serovadasha272
Предмет: Английский язык,
автор: serovadasha272