Предмет: Геометрия,
автор: Danyakashka
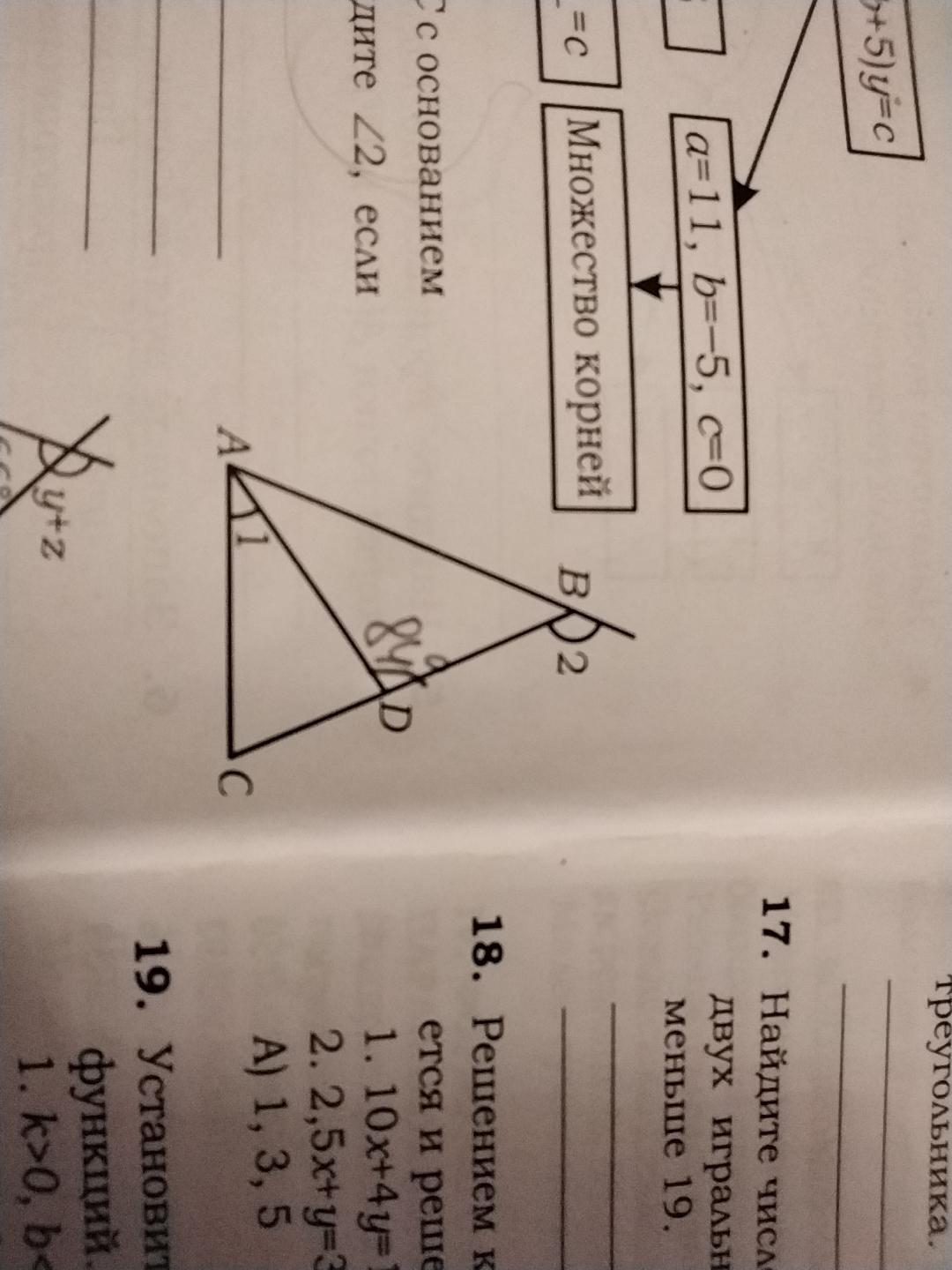
В равнобедренном треугольнике ABC с основанием AC проведена биссектриса AD. Найдите угол 2 если уголADB=84градусов , угол2=4×угол 1
Приложения:
Ответы
Автор ответа:
2
Ответ:
∠2 = 112°
Объяснение:
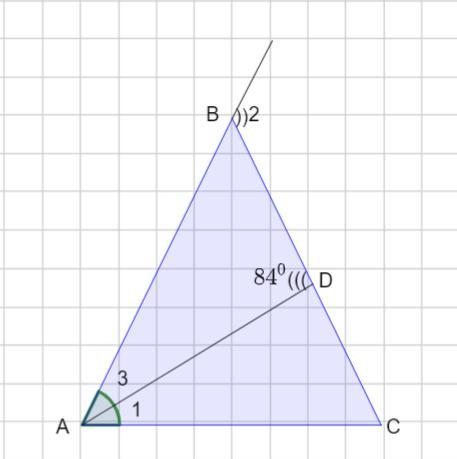
В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. Найдите угол 2, если угол ADB равен 84°, угол 2 равен 4× угол 1.
По условию дан ΔАВС -равнобедренный . AD - биссектриса.
Тогда ∠1 = ∠3 ( так как биссектриса делит угол пополам)
∠ 2 - внешний угол Δ АВС при вершине В. По условию ∠2= 4 · ∠1.
Рассмотрим Δ АDВ, ∠ 2 - внешний угол.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Значит, ∠ 2 = ∠3 + ∠ADB.
Пусть градусная мера ∠ 1 = х. Тогда ∠3 = ∠1 = х, а ∠2 =4х.
Составим уравнение:
4х= х + 84°;
4х - х =84°;
3х =84°;
х = 84° : 3 ;
х = 28°
Значит, ∠ 1 = 28°.
Найдем ∠2
∠2= 4· 28° = 112°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: gmiaeva05
Предмет: Химия,
автор: galanov54ivan
Предмет: Английский язык,
автор: milana94587
Предмет: Математика,
автор: cherry1527