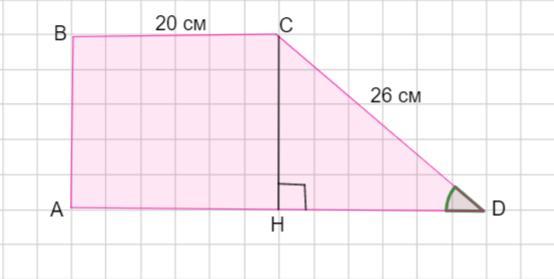
Більша бічна сторона прямокутної трапеції дорівнює 26 см, а менша основа - 20 см. Знайдіть площу трапеції, якщо 12/5 тангенс гострого кута при основі дорівнює

Ответы
Ответ:
600 см ²
Пошаговое объяснение:
Большая боковая сторона прямоугольной трапеции равна 26 см, меньшее основание 20 см. Найти площадь трапеции, если тангенс острого угла при основание 12/5.
Пусть дана прямоугольная трапеция АВСD.
СD =26 см, ВС =20 см ,
Проведем высоту СН. Тогда Δ СНD - прямоугольный.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Так как нет ни одного катета, то воспользуемся формулой
и определим косинус ∠D.
так как угол острый.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
см
Найдем CH через тангенс
см
АВСН - прямоугольника. У прямоугольника противолежащие стороны равны. Значит, АН =ВС = 20 см.
АD= АН +НD;
АD =20 + 10 = 30 см.
Найдем площадь трапеции как произведение полусуммы оснований на высоту.
Значит, площадь трапеции равна 600 см ².
#SPJ1