Question

Середня лінія трикутника відтинає від нього трапецію, площа якої 21см² Знайдіть площу даного трикутника.

Answer 1

Ответ:

Площа трикутника дорівнює 28 см²

Пошаговое объяснение:

Середня лінія трикутника відтинає від нього трапецію, площа якої 21см² Знайдіть площу даного трикутника.

Розв'язання.

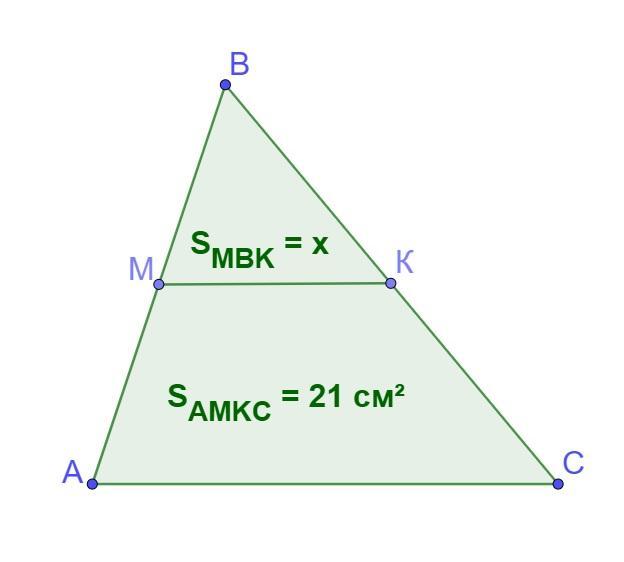
Нехай АВС - заданий трикутник. МК - середня лінія, що сполучає середини сторін AB і BC, відповідно.

За умовою  MК відтинає від трикутника ABC трапецію AMКС, площа якой 21 см².

ΔАВС~ΔМВК за двома кутами:

• АС ║МК (за властивістю середней лінії), тому ∠А=∠ВМК - як відповідні кути
• ∠В - спільний

Так як відношення площ подібних трикутників пропорційне квадрату лінійних розмірів відповідних сторін, маємо:

$\bf \dfrac{S_{ABC}}{S_{MBK}} =\dfrac{AC^{2} }{MK^{2} }$

Нехай площа ΔМВК дорівнює х, тоді площа ΔАВС дорівнює х+21.

АС = 2МК - за властивістю середней лінії трикутника. Маємо:

$\dfrac{x+21}{x} =\dfrac{(2MK)^{2} }{MK^{2} }$

$\dfrac{x+21}{x} =\dfrac{4MK^{2} }{MK^{2} }$

$\dfrac{x+21}{x} =\dfrac{4 }{1}$

4x=x+21

3x=21

x=7

Отже, площа ΔАВС:  7+21 = 28 (см)²

#SPJ1