Предмет: Алгебра,
автор: maximvehetek
Знайти похідні функції
Приложения:
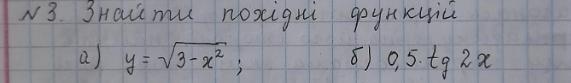
Ответы
Автор ответа:
0
Решение.
Производные функций находим по правилам дифференцирования .
Производная сложной функции равна производной внешней функции, умноженной на производную внутренней функции .
Приложения:
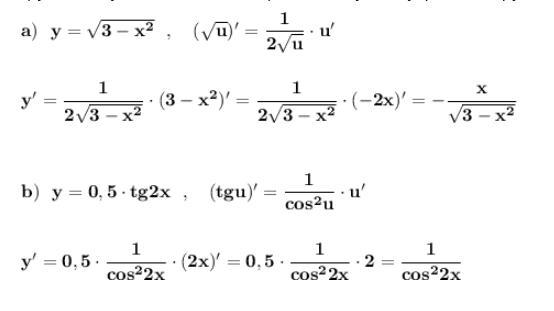
Похожие вопросы
Предмет: Литература,
автор: elizavetasaar
Предмет: Литература,
автор: Dasherak666
Предмет: Физика,
автор: katyaparch
Предмет: Немецкий язык,
автор: yarikVodila12986
Предмет: Английский язык,
автор: iamdinozavrik488