Question

СРОЧНО!!

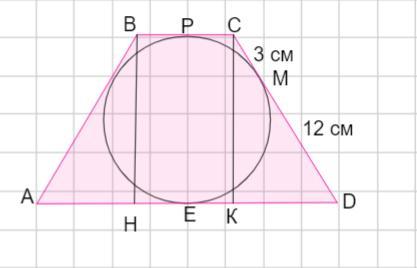
Точка дотику кола, вписаного у рівнобічну трапецію, ділить бічну сторону на відрізки 12 см і 3 см. Знайдіть площу трапеції.

Answer 1

Ответ:

180 см ².

Объяснение:

Точка касания окружности, вписанной в равнобедренную трапецию, делит боковую сторону на отрезки 12 см и 3 см. Найти площадь трапеции.

Пусть дана трапеция АВСD - равнобедренная. АВ = СD.

Точка М - точка касания вписанной окружности боковой стороны СD.

СМ = 3 см, МD =12 см. Тогда СD = СМ +МD =3 +12 =15 см.

Так как трапеция равнобедренная , то АВ = СD =15 см.

Если окружность вписана в четырехугольник, то суммы противолежащих сторон равны .

ВС +АD=АВ+ СD =15 +15 =30 см.

Площадь трапеции равна произведению полусуммы оснований на высоту трапеции.

Если точка Р - точка касания окружности с основанием Вс. Так как отрезки касательных равны , то СР =СМ = 3 см. Тогда ВС = 6 см .

Если точка Е  -точка касания окружности с основанием АD. Тогда DК=DМ = 12 см и основание АD =24 см.

Проведем высоты ВН и СК.

Если трапеция равнобедренная, то АН =КD.

НВСК - прямоугольник. НК =ВС =6 см .

АН =КD = (24 -6): 2 = 18 : 2 = 9 см.

Рассмотрим ΔАНВ - прямоугольный и применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

ВН ²= АВ² -  АН²;

ВН² = 15²- 9² = 225 - 81 = 144;

ВН = √144 = 12 см.

Тогда площадь трапеции будет

$S =\dfrac{BC +AD}{2} \cdot BH;\\\\S =\dfrac{30}{2} \cdot 12= 15\cdot12 =180$

Значит, площадь трапеции равна 180 см ².

#SPJ1