Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста решить задачу , очень срочно
Приложения:
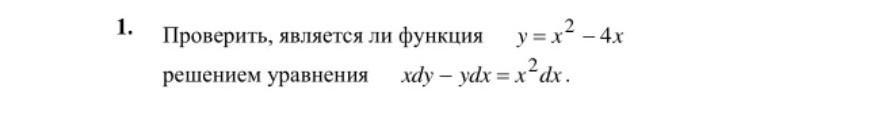
Ответы
Автор ответа:
1
Ответ:
Задано дифференциальное уравнение :
.
Проверим, является ли функция решением этого уравнения .
Найдём производную .
Подставим функцию в уравнение :
Равенство выполняется, значит указанная функция является решением заданного дифференциального уравнения .
Приложения:

masha01021:
спасибо большое
очень благодарна
можете еще раз помочь
последний раз
Похожие вопросы
Предмет: Химия,
автор: verzevskadasa
Предмет: Геометрия,
автор: basistaa2001
Предмет: Математика,
автор: miviksii
Предмет: Алгебра,
автор: thesia122002
Предмет: Немецкий язык,
автор: fotiku96