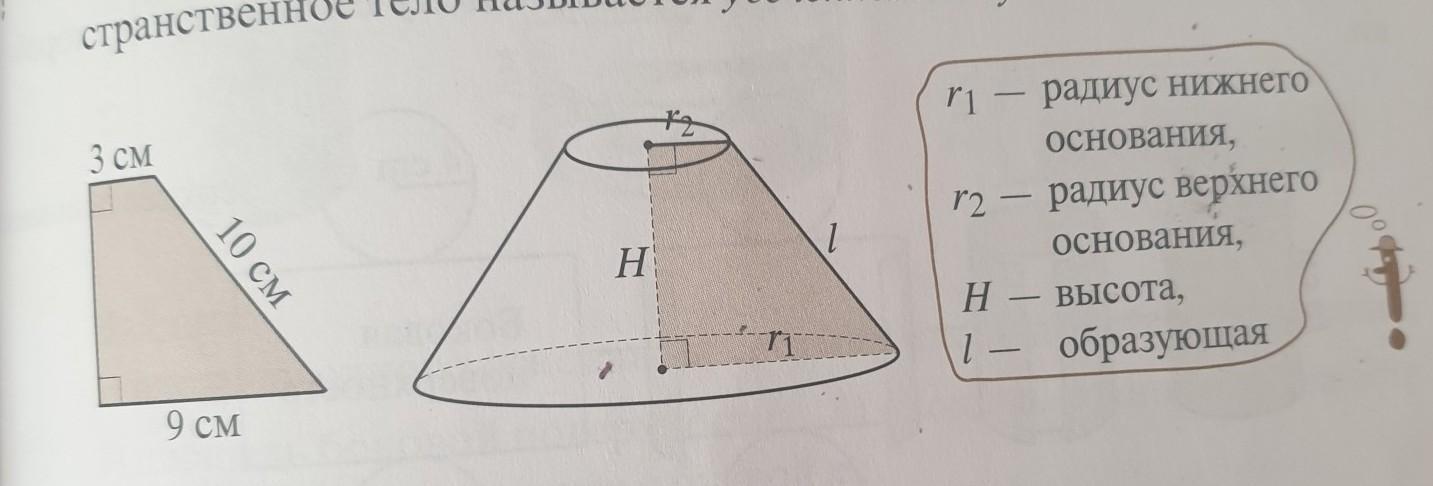
359. Прямоугольную трапецию (см. рис. слева)
вращают вокруг боковой стороны, которая перпендикулярна основаниям. Полученное пространственное тело называется усеченным конусом.
1) Чему равна длина:
а) радиуса нижнего основания r1?
б) радиуса верхнего основания r2?
в) образующей l?
2) Найдите длины окружностей оснований и их площади. Ответ запишите с буквой п.
3) Найдите высоту Н усеченного конуса.
Ответы
Ответ:
Я тобі дам відповідь на це питання, також расскажу як його робити, але це невірно, тоді пробач.
Длина радиуса нижнего основания r1:
Радиус нижнего основания соответствует половине длины его диагонали.
По теореме Пифагора, диагональ равна sqrt(AB^2 + BC^2), где AB и BC - стороны прямоугольника.
Диагональ равна sqrt(5^2 + 12^2) = sqrt(25 + 144) = sqrt(169) = 13.
Так как радиус равен половине диагонали, то r1 = 13/2 = 6.5 см.
Длина радиуса верхнего основания r2:
Радиус верхнего основания равен половине длины его диагонали.
По теореме Пифагора, диагональ равна sqrt(CD^2 + DA^2), где CD и DA - стороны прямоугольника.
Диагональ равна sqrt(8^2 + 15^2) = sqrt(64 + 225) = sqrt(289) = 17.
Так как радиус равен половине диагонали, то r2 = 17/2 = 8.5 см.
Длина образующей l:
Образующая l представляет собой расстояние между верхней и нижней точками конуса.
В данном случае, это равно высоте прямоугольной трапеции.
Высота трапеции равна BC = 12 см.
Длины окружностей оснований и их площади:
Окружность основания с радиусом r1:
Длина окружности основания = 2 * π * r1 = 2 * π * 6.5 = 13π см.
Площадь окружности основания = π * r1^2 = π * 6.5^2 = 42.25π см^2.
Окружность верхнего основания с радиусом r2:
Длина окружности верхнего основания = 2 * π * r2 = 2 * π * 8.5 = 17π см.
Площадь окружности верхнего основания = π * r2^2 = π * 8.5^2 = 72.25π см^2.
Высота H усеченного конуса:
Высота H соответствует высоте прямоугольной трапеции, которая равна 5 с
Пошаговое объяснение: