Предмет: Геометрия,
автор: Art016
Відрізок RV — висота рівнобедреного трикутника CRM (CR=RM). На стороні
CR позначили точку F так, що FV||RM. Доведіть, що FB = FV.
Ответы
Автор ответа:
0
Ответ:
Довели, що FR=FV
Объяснение:
Уточнена умова:
Відрізок RV — висота рівнобедреного трикутника CRM (CR=RM). На стороні CR позначили точку F так, що FV||RM. Доведіть, що FR = FV.
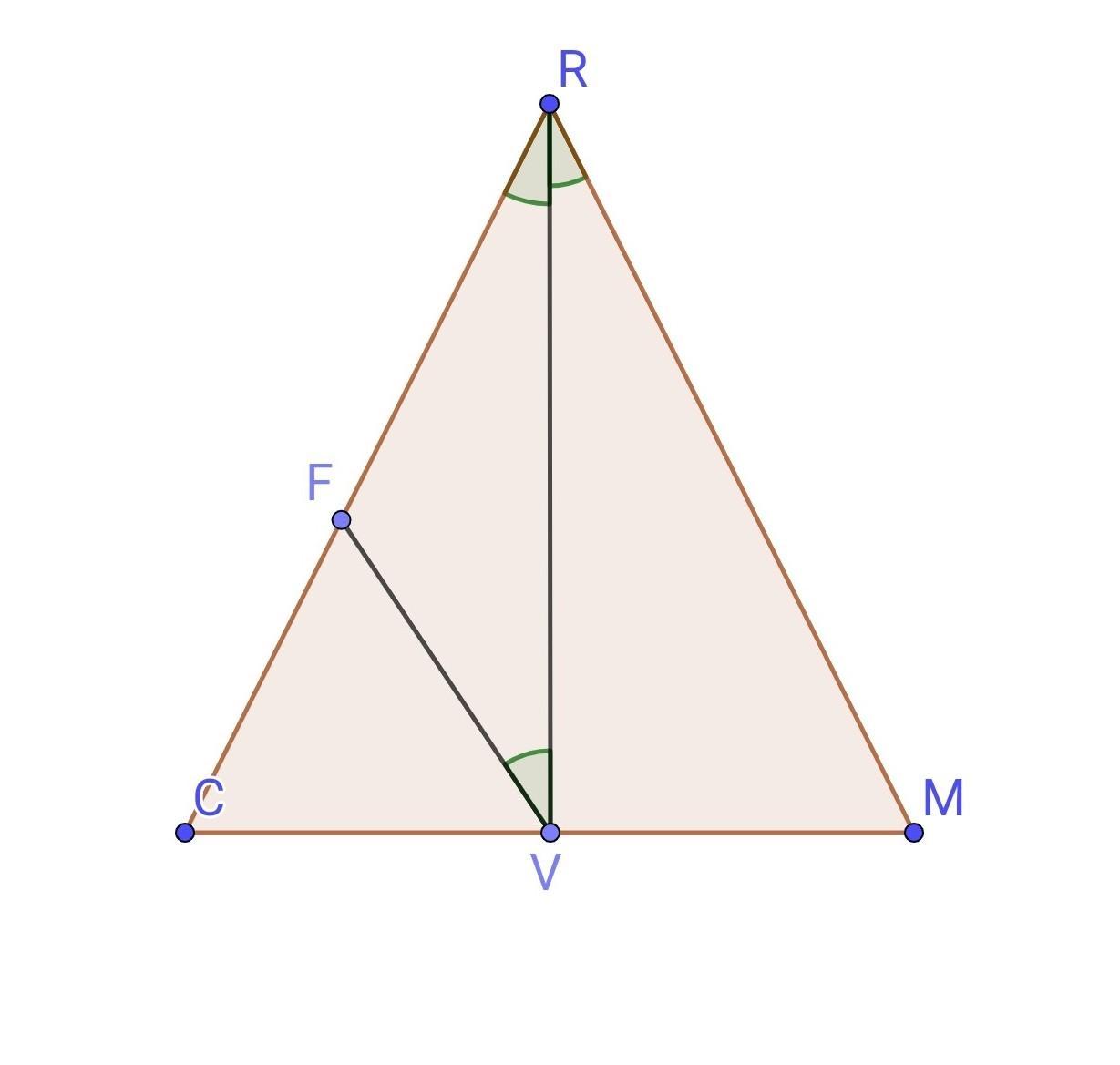
Дано: △CRM, CR=RM, RV⟂CM, F ∈ CR, FV || RM.
Довести: FR=FV.
Доведення
Так як в рівнобедреному трикутнику висота буде також бісектрисою, то:
∠VRM=∠VRC.
∠VRM=∠FVR - як внутрішні різносторонні кути при перетині паралельних прямих FV і RM січною RV.
Отже ∠VRC=∠FVR, тому △VFR - рівнобедрений з основою RV.
Тому FR=FV - як бічні сторони рівнобедреного трикутника.
Що і треба було довести.
#SPJ1
Приложения:
Похожие вопросы