Допоможіть будь ласка!!

Ответы
Ответ:
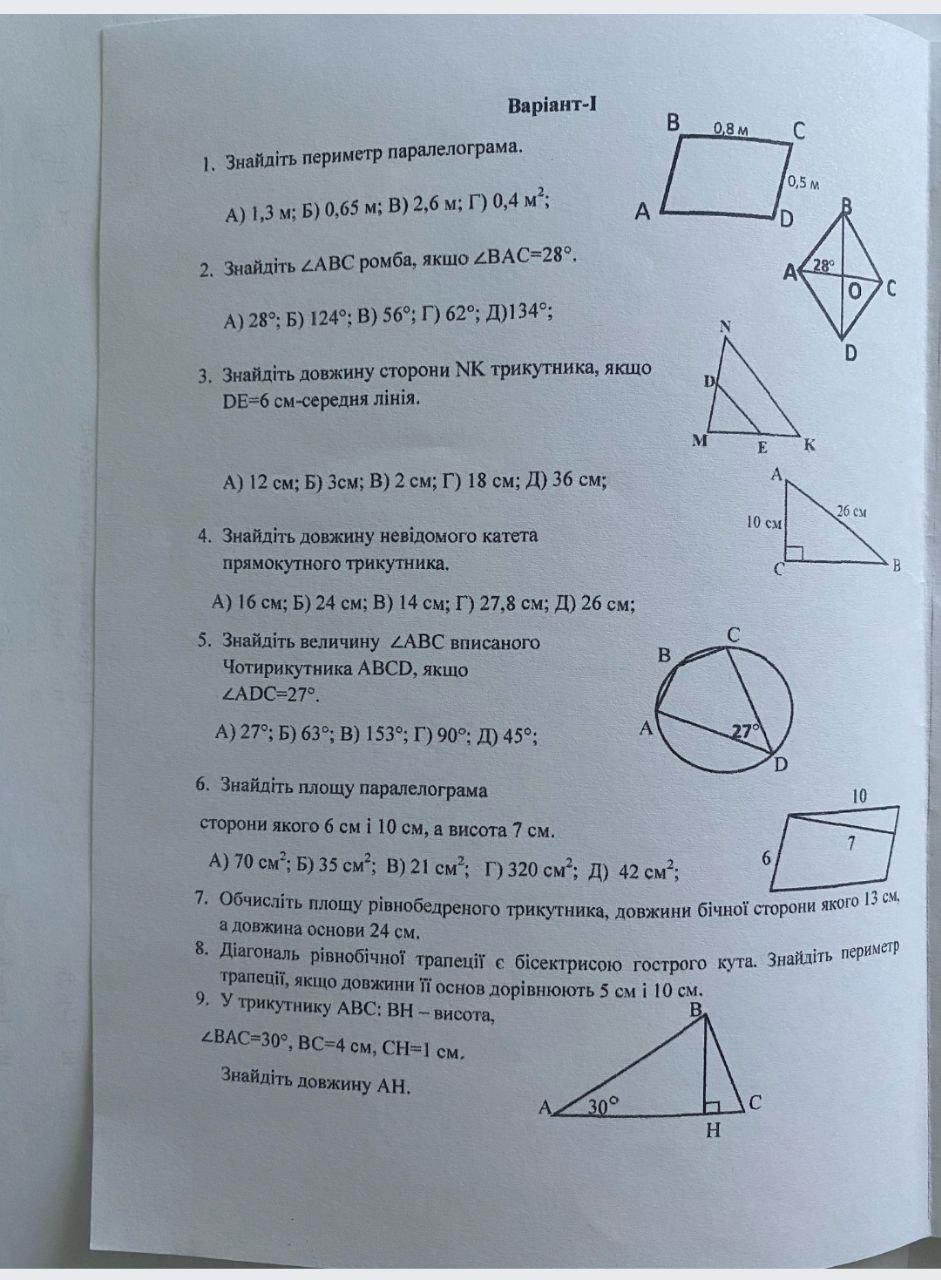
1.Периметр паралелограма ABCD складається з суми довжин його сторін. За умовою, сторона BC дорівнює 0,8 метра, а сторона CD дорівнює 0,5 метра. Оскільки паралелограм має протилежні сторони паралельні і рівні, то сторона AB дорівнює BC, а сторона DA дорівнює CD. Тому:
AB = BC = 0,8 м
DA = CD = 0,5 м
Отже, периметр паралелограма ABCD дорівнює:
P = AB + BC + CD + DA = 0,8 м + 0,8 м + 0,5 м + 0,5 м = 2,6 метра
Відповідь: периметр паралелограма ABCD дорівнює 2,6 метра
Відповідь: В)
2.У ромбі протилежні кути рівні, тому кут ВАС дорівнює куту ВСА. Оскільки сума кутів трикутника дорівнює 180 градусів, то кути ВАС і ВСА разом дорівнюють 180 - 28 = 152 градусам.
Ромб має дві паралельні сторони, тому кути, які лежать між цими сторонами, рівні. Отже, кут АBC дорівнює куту ВАС, тобто 28 градусам.
Отже, кут ABC ромба дорівнює 28 градусам.
Відповідь: А)
3.За теоремою Піфагора для правильного трикутника сторона, що ділить його на два рівні трикутники (у нашому випадку - DE), дорівнює:
DE = (сторона / 2) * √2.
Підставляючи дані з задачі, маємо:
6 = (сторона / 2) * √2.
Розв'язуємо рівняння відносно сторони:
сторона = 6 * 2 / √2 = 12√2.
Отже, довжина сторони NK трикутника MNK дорівнює 12√2.
12√2=12×≈1,5=18см
Відповідь:Г)
4.За теоремою Піфагора довжина невідомого катета CB прямокутного трикутника ABC може бути знайдена за формулою:
CB = √(AB² - CA²)
Підставляючи відповідні значення, отримаємо:
CB = √(26² - 10²)
CB = √(676 - 100)
CB = √576
CB = 24 см
Отже, довжина невідомого катета CB дорівнює 24 см.
Відповідь: Б)
5.Для того, щоб знайти кут ABC вписаного чотирикутника ABCD, якщо кут ADC=27°, нам потрібно скористатися теоремою про кут вписаного чотирикутника, яка стверджує, що сума протилежних кутів вписаного чотирикутника дорівнює 180 градусам.
Оскільки кут ADC вже відомий та дорівнює 27°, то протилежний йому кут ABC дорівнює
180° - 27° = 153°.
Таким чином, отримуємо, що кут ABC вписаного чотирикутника ABCD дорівнює 153°
Відповідь: В)
6.За формулою для площі паралелограма, S = a * h, де а - довжина основи, а h - висота, можна знайти площу паралелограма.
Таким чином, S = 6 см * 7 см = 42 кв.см.
Відповідь: Д)
7.Розглянемо рівнобедрений трикутник з бічною стороною 13 см і двома однаковими бічними сторонами, які мають довжину х. Оскільки трикутник рівнобедрений, то його висота опущена на основу і ділить її на дві рівні частини. Тому:
24/2 = 12 см - довжина висоти.
Застосовуючи формулу для площі трикутника:
S = 1/2*a*h = 1/2*24*12 = 144 кв. см.
Отже, площа рівнобедренного трикутника дорівнює 144 кв. см.
8.Позначимо вершину трапеції гострим кутом як A, а вершину протилежну до неї - як B. Тоді діагональ AC є бісектрисою кута A, і вона ділить сторону BC на дві рівні частини. Оскільки трапеція рівнобічна, то сторона AB також ділиться діагоналею AC на дві рівні частини. Позначимо точку ділення BC на дві рівні частини як D.
Тоді відрізок BD має довжину 5/2 см, а відрізок CD має довжину 10/2 = 5 см. Відрізок AC є бісектрисою кута A, тому AD = DC.
Позначимо довжину бічної сторони трапеції як х. За теоремою Піфагора для прямокутного трикутника ACD маємо:
AC^2 = AD^2 + CD^2 = x^2
А за теоремою Піфагора для прямокутного трикутника BCD маємо:
BD^2 = BC^2 - CD^2 = (x + 5)^2 - 25
Оскільки діагональ AC є бісектрисою кута A, то кути ACD і ACB є рівними, тобто трикутник ABC є рівнобедреним, і ми можемо записати:
AB = BC = x + 5
Отже, периметр трапеції дорівнює:
P = AB + BC + CD + DA = (x + 5) + (x + 5) + 5 + 2x = 4x + 15
З іншого боку, ми знаємо, що діагональ AC є бісектрисою кута A, тому кути BCD і ACD є рівними, тобто трикутник BCD є рівнобедреним. Звідси випливає, що BD = CD = 5 см. Підставляючи це вираз для BD^2, отримуємо:
BD^2 = (x+5)^2 - 25 = 25
x^2 + 10x = 0
х(x+10) = 0
x = 0 або x = -10
Очевидно, що довжина сторони трапеції не може бути від'ємною, тому єдиним допустимим розв'язком є x = 0 см. Отже, периметр трапеції дорівнює:
P = 4x + 15 = 15 см.