Предмет: Математика,
автор: julsi32
Решите пожалуйста!!
cos^2x=5-5sinx
Приложения:

Ответы
Автор ответа:
0
Ответ:
Решить уравнение . Применяем основное тригонометрическое
тождество : .
Приложения:
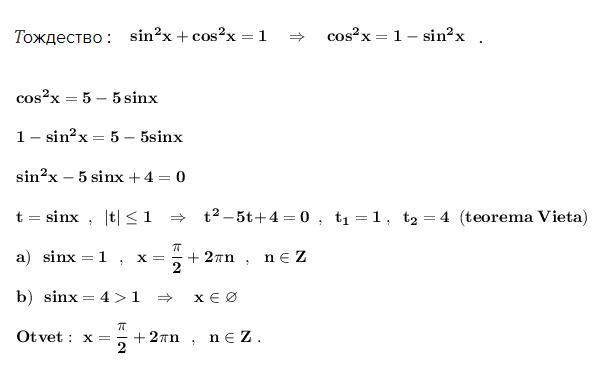
Похожие вопросы
Предмет: Математика,
автор: sargorodskaaviktoria
Предмет: Информатика,
автор: omagalPOCJ
Предмет: Алгебра,
автор: sofiaboiko2009
Предмет: Алгебра,
автор: raminamalmakova
Предмет: Биология,
автор: njyygfde