Предмет: Алгебра,
автор: schauder
Помогите решить, пожалуйста :3
1) 7sin^2x+3sinx*cosx-2cos^2x=4
2) sin2x=2cos^2x
Ответы
Автор ответа:
0
1) 7sin^2(x) + 3sinx*cosx - 2cos^2(x) - 4sin^2(x) - 4cos^2(x) = 0
3sin^2(x) + 3sinx*cosx - 6cos^2(x) = 0
tg^2(x) + tgx - 2 = 0
tgx = -2, x=-arctg(2) + πk
tgx = 1, x=π/4 + πk
2) sin(2x) = 2cos^2(x)
2sinx*cosx - 2cos^2(x) = 0
2cosx*(sinx - cosx) = 0
cosx = 0, x=π/2 + πk
sinx=cosx, tgx = 1, x=π/4 + πk
3sin^2(x) + 3sinx*cosx - 6cos^2(x) = 0
tg^2(x) + tgx - 2 = 0
tgx = -2, x=-arctg(2) + πk
tgx = 1, x=π/4 + πk
2) sin(2x) = 2cos^2(x)
2sinx*cosx - 2cos^2(x) = 0
2cosx*(sinx - cosx) = 0
cosx = 0, x=π/2 + πk
sinx=cosx, tgx = 1, x=π/4 + πk
Автор ответа:
0
Думаю ответ таков,но незнаю ли то...
Приложения:
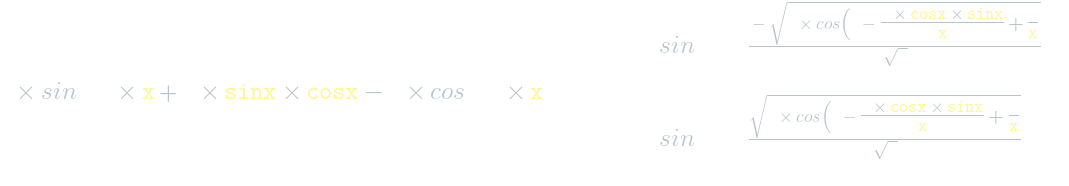

Похожие вопросы
Предмет: История,
автор: kissavladozbbk4
Предмет: Обществознание,
автор: ZlatkaChocolade
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: макас666
Предмет: Математика,
автор: TomaDoroz