Предмет: Геометрия,
автор: dtstvhocup
Площа осьового перерізу конуса дорівнює 4 √3 см2. Знайдіть обʼєм конуса, якщо його твірна утворює із площиною основи кут 30°
Ответы
Автор ответа:
1
Ответ:
8π см³
Объяснение:
Площадь осевого сечения конуса равна 4√3 см². Найти объем конуса, если его образующая образует с плоскостью основания угол 30°.
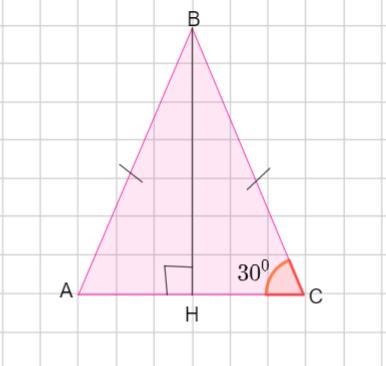
Пусть дан ΔАВС - равнобедренный - осевое сечение конуса. ВН - высота конуса.
По условию площадь этого треугольника равна 4√3 см².
Пусть радиус основания конуса будет х см, то есть АН = НС = х см.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тогда в ΔВНС - прямоугольном найдем тангенс ∠С.
Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне
Значит, радиус основания конуса R = 2√3 cм ,
а высота cм.
Объем конуса определяется по формуле
см³.
Тогда объем конуса равен 8π см³
#SPJ1
Приложения:
Похожие вопросы
Предмет: Химия,
автор: sagalievadilnaz6
Предмет: Физика,
автор: aleksandrnovikov3211
Предмет: Окружающий мир,
автор: mikon1171
Предмет: Немецкий язык,
автор: zhannochkakruglova
Предмет: Геометрия,
автор: coolsanyanomer1