Question

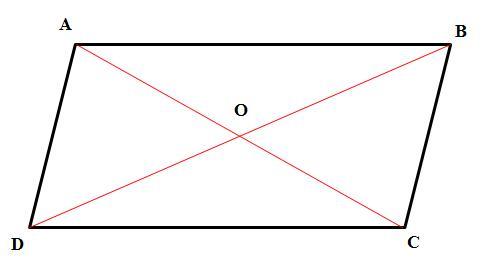
У паралелограмі ABCD задано координати вершин А(5;3) В( -4;1) а також точки перетину діагоналей О(0; -3) знайти координати вершин С і Д а також периметер ​

Answer 1

Ответ:

Координаты вершин: С(-5; -9) и D(4; -7)

Периметр параллелограмма равен $\tt 2 \cdot (\sqrt{85}+\sqrt{101} )$ (ед.)

Объяснение:

Перевод: В параллелограмме ABCD заданы координаты вершин А(5;3) и В(-4; 1), а также точки пересечения диагоналей О(0; -3). Найти координаты вершин С и D, а также периметр.

Информация: 1) Координаты (x₀; y₀) середины отрезка MN определяются по формуле:

$\tt x_0=\dfrac{x_M+x_N}{2}, \;\; y_0=\dfrac{y_M+y_N}{2},$

здесь $\tt M(x_M; y_M)$ и $\tt N(x_N; y_N)$.

2) Расстояние между точками $\tt M(x_M; y_M)$ и $\tt N(x_N; y_N)$ определяется по формуле: $\tt d(MN)=\sqrt{(x_M-x_N)^2+(y_M-y_N)^2}$.

3) Периметр параллелограмма определяется по формуле: P=2·(a+b), где a и b - смежные стороны.

Решение. Так как в параллелограмме диагонали делятся пополам точкой пересечения диагоналей, то точка О(0; -3) является серединой отрезка AC и отрезка BD.

Тогда верны равенства

$\tt x_O=\dfrac{x_A+x_C}{2}, \;\; y_O=\dfrac{y_A+y_C}{2}, \\\\x_O=\dfrac{x_B+x_D}{2}, \;\; y_O=\dfrac{y_B+y_D}{2}.$

Подставим известные координаты:

$\tt 0=\dfrac{5+x_C}{2}, \;\; -3=\dfrac{3+y_C}{2}, \\\\ 0=\dfrac{-4+x_D}{2}, \;\; -3=\dfrac{1+y_D}{2}.$

Отсюда

$\tt x_C=0 \cdot 2-5=-5, \;\; y_C=-3 \cdot 2-3=-9, \\\\ x_D=0 \cdot 2+4=4, \;\; y_D=-3 \cdot 2-1=-7.$

Теперь определим длины смежных сторон AB и AD параллелограмма:

$\tt d(AB)=\sqrt{(5-(-4))^2+(3-1)^2}=\sqrt{9^2+2^2}=\sqrt{81+4}=\sqrt{85}, \\\\ d(AD)=\sqrt{(5-4)^2+(3-(-7))^2}=\sqrt{1^2+10^2}=\sqrt{1+100}=\sqrt{101}.$

Остаётся вычислить периметр параллелограмма:

$\tt P=2 \cdot (\sqrt{85}+\sqrt{101} ).$

#SPJ1