Предмет: Алгебра,
автор: vghyne
помогите пожалуйста!!
Приложения:
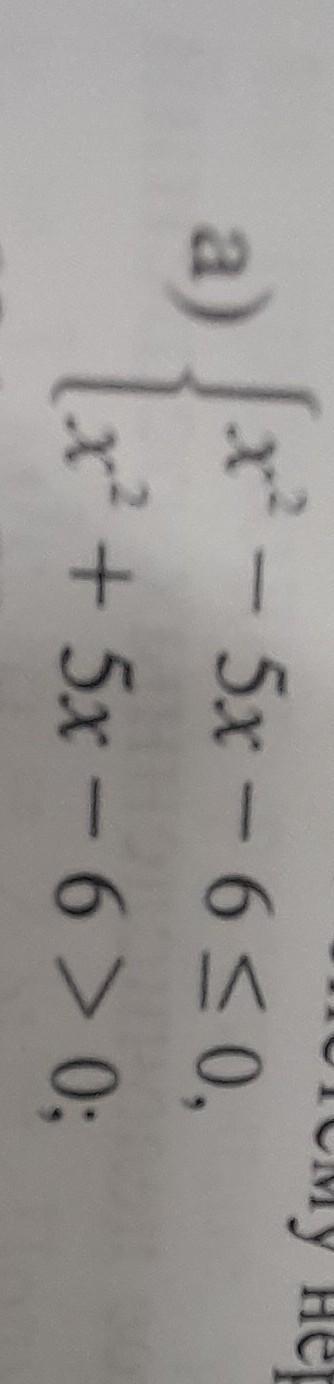
Ответы
Автор ответа:
0
Решение.
Разложим квадратные трёхчлены на множители . Для этого нужно найти их корни .
По теореме Виета корни квадр. трёхчлена связаны
соотношениями .
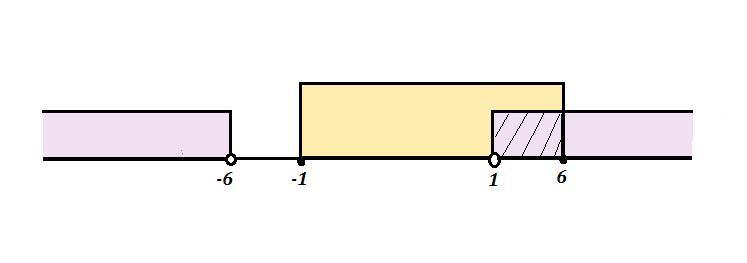
Теперь решим неравенства методом интервалов .
Ответ: х ∈ ( 1 ; 6 ] .
Приложения:

Похожие вопросы
Предмет: Химия,
автор: gerasimenkoafina
Предмет: Английский язык,
автор: skyba0
Предмет: Химия,
автор: term292928
Предмет: Русский язык,
автор: Olgarfcv
Предмет: Математика,
автор: MolkyWay