Предмет: Математика,
автор: book000
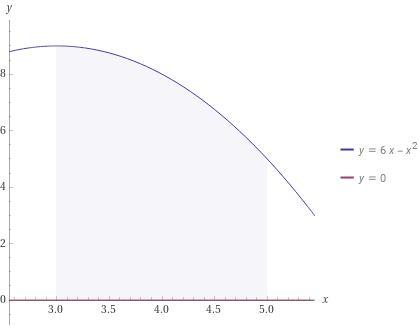
Найти площадь криволинейной трапеции, ограниченной прямыми х=3, x=5, графиком y=6x-x² и осью ОХ
Ответы
Автор ответа:
1
Відповідь:
Покрокове пояснення:
Приложения:
Похожие вопросы
Предмет: Химия,
автор: cuteblonde
Предмет: Литература,
автор: sashabdkdr
Предмет: Алгебра,
автор: zefirro4ka
Предмет: Алгебра,
автор: 0985622310
Предмет: Биология,
автор: madamkpvap