Предмет: Алгебра,
автор: svischoyulianna
Виконайте даю 40 балів
Приложения:
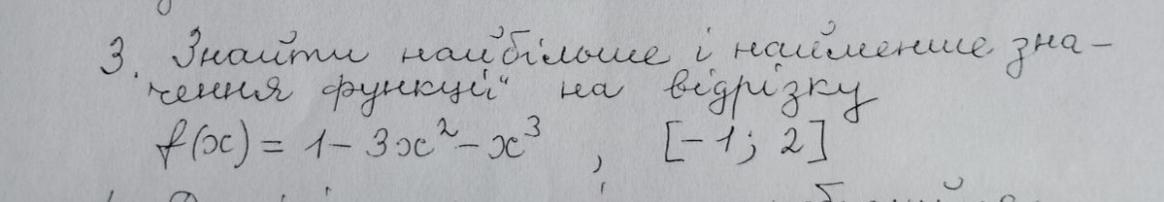
Ответы
Автор ответа:
0
Ответ.
Найдём критические (стационарные) точки .
Вычислим значения функции в критических точках и на концах сегмента .
Выбираем наименьшее и наибольшее значения .
Наименьшее значение : .
Наибольшее значение : .
Приложения:

Похожие вопросы