Предмет: Геометрия,
автор: xiixodila
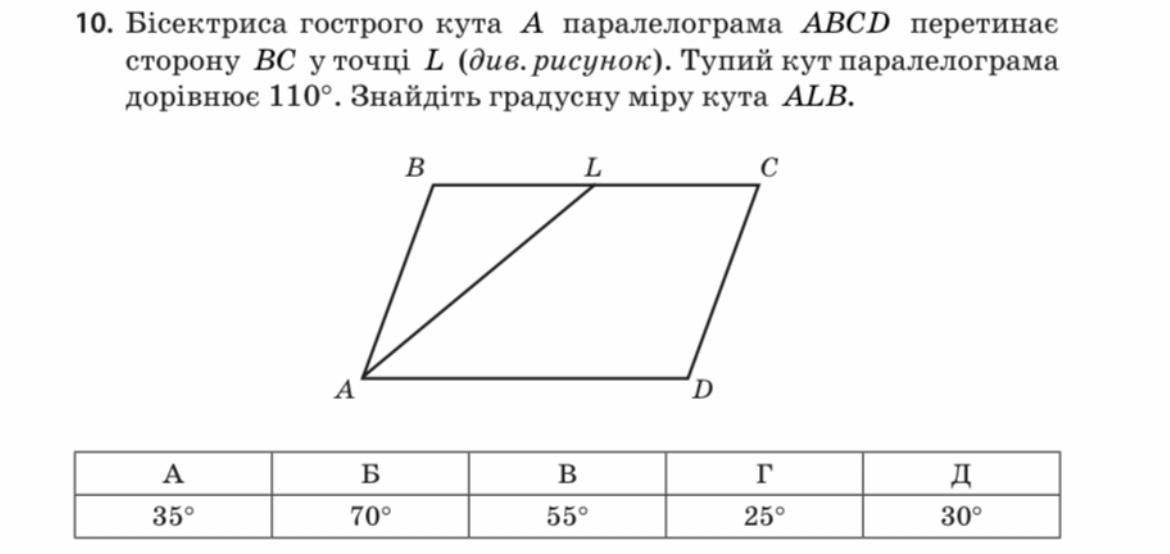
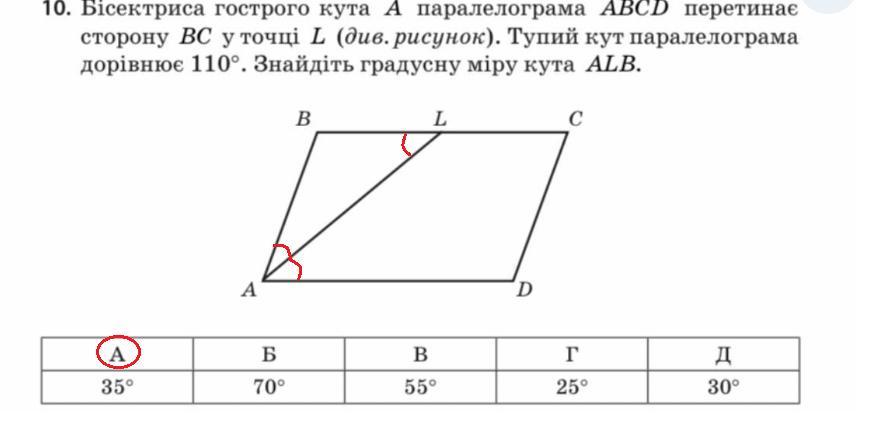
Биссектриса острого угла А параллелограмма ABCD пересекает сторону ВС в точке L (см. рисунок). Тупой угол параллелограмма равен 110°. Найдите градусную меру угла ALB.
Приложения:
ГАЗ52:
35°
Ответы
Автор ответа:
2
Ответ:
∠АLВ =35°.
Объяснение:
Биссектриса острого угла А параллелограмма ABCD пересекает сторону ВС в точке L . Тупой угол параллелограмма равен 110°. Найти градусную меру угла АLВ.
Дан параллелограмм ABCD, ∠В =110°, АL - биссектриса.
Если АL - биссектриса, то ∠ВАL =∠LАD.
∠LАD= ∠АLВ как накрест лежащие, образованные ВС ║АD и секущей АL.
Тогда ∠ВАL= ∠АLВ и в ΔАLВ два угла равны и он равнобедренный.
Сумма углов треугольника равна 180°. Если ∠В =110°, то
∠ВАL= ∠АLВ = (180° - 110°): 2 = 70° : 2 =35°.
Тогда ∠АLВ =35°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: krasnovadasa78
Предмет: Английский язык,
автор: anutavalion2008
Предмет: Английский язык,
автор: f2ckf4kesh1t
Предмет: Українська мова,
автор: bogdan1742