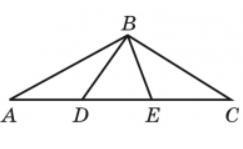
На рисунку AD=BD, BE=CE, ∠BDE=50°; ∠BED=40°. Найдите угол ABC.
Развернутый ответ, пожалуйста.
Ответы
Ответ:
Рассмотрим треугольник АВD
По условию задачи АD=BD,значит
треугольник равнобедренный, и его углы при основании равны между собой
Для начала найдём угол при вершине этого треугольника
<АDB+<BDE=180 градусов,как смежные
<АDB=180-50=130 градусов
<А=<АВD=(180-130):2=25 градусов
Рассмотрим треугольник ВЕС,он тоже равнобедренный,т к ВЕ=СЕ,по условию задачи,а это боковые стороны треугольника
Найдем угол при вершине треугольника
<ВЕС+<ВЕD=180 градусов,как смежные
<ВЕС=180-40=140 градусов
Углы при основании
Равнобедренного треугольника равны между собой
<С=<ЕВС•(180-140):2=20 градусов
Теперь мы можем ответить на поставленный вопрос-узнать,чему равен <АВС
180-(20+25)=135 градусов
Мы можем проверить себя
Для этого узнаем угол при вершине треугольника DBE,нам же по условию задачи известны два его угла
<DBE=180-(50+40)=90 градусов
<АВС=<АВD+<DBE+<EBC=
=25+90+20=135 градусов
Решение верное!!!
Объяснение: