Предмет: Алгебра,
автор: tomabaybotagoz
срочно пж нужно дам 50 баллов
Приложения:
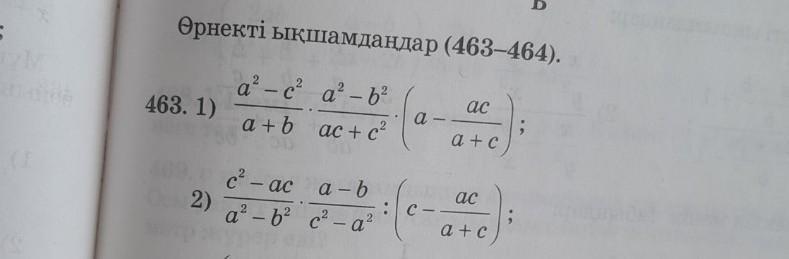
Ответы
Автор ответа:
1
1)
2)
Похожие вопросы
Предмет: Українська мова,
автор: alexuchirov1306
Предмет: Химия,
автор: china433
Предмет: Алгебра,
автор: nastinnes
Предмет: Физика,
автор: DimaXtwin