Question

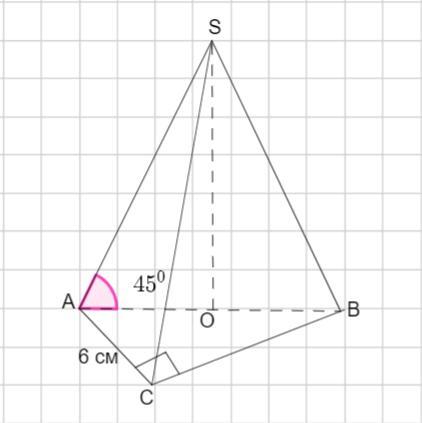
Площа основи піраміди 24 см².В основі лежить прямокутний трикутник найменша сторона якого 6 см. Усі бічні ребра нахилені до площини основи під кутом 45°. Знайдіть висоту піраміди

Answer 1

Ответ:

5 см.

Пошаговое объяснение:

Площадь основания пирамиды 24 см ². В основании лежит прямоугольный треугольник, меньшая сторона которого равна 6 см. Все боковые ребра наклонены к плоскости основания под углом 45 °. Найти высоту пирамиды.

Пусть дана пирамида SABC. ΔАВС - прямоугольный, ∠С =90 °,

АС = 6 см.  S(ΔАВС) =24 см ².

Площадь прямоугольного треугольника равна полупроизведению катетов .

Тогда

$S = \dfrac{1}{2} \cdot A C \cdot BC ;\\\\24= \dfrac{1}{2} \cdot 6 \cdot BC;\\\\24 = 3\cdot BC ;\\\\BC = 24:3;\\\\BC =8$

Катет ВС = 8 см.

Найдем гипотенузу по теореме Пифагора :  в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

АВ ²= АС ² +ВС²;

АВ ² = 6² +8² = 36+ 64 =100

АВ = √100 = 10 см

Так как все боковые ребра наклонены под одним углом, то вершина проектируется в центр, описанной около ΔАВС,  окружности. А для прямоугольного треугольника - это середина гипотенузы, то есть точка О - середина АВ.

Рассмотрим Δ АОS - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90 °.

Если ∠SАО =45 °, то ∠АSО =90° - 45 °= 45°

Если в треугольнике два угла равны, то он равнобедренный.

Δ АОS - прямоугольный, равнобедренный.

SО =АО = АВ : 2 =10: 2 =5 см.

Значит, высота пирамиды равна 5 см.

#SPJ1